Persamaan linear dan fungsi linear

Tentu kita sudah mengetahui tentang suatu persamaan. Atau kita masih bingung mengenai perbedaan suatu persamaan dengan kesamaan. Apa itu persamaan dan apa iu kesamaan? Coba kita perhatikan dua hal ini.
  
dan

  
Manakah yang merupakan persamaan dan manakah yang merupakan suatu kesamaan? Dengan contoh tersebut kita akan lebih mudah mengetahui perbedaannya. adalah
merupakan suatu persamaan. Mengapa? Ini karena didalamnya ada suatu variable. Sedangkan yang kedua adalah suatu kesamaan. Karena sudah sangatlah jelas bahwa ruas sebelah kanan sama dengan ruas di sebelah kiri. Atau bisa juga dikatakan karena didalamnya tidak ada suatu variable. Sudah jelas perbedaan antara persamaan dengan kesamaan. Tentunya kita pasti akan mengetahuinya secara tidak langsung mengenai pertidaksamaan, pertaksamaan, atau ketaksamaan.
  
Sekarang bagaimana menyelesaikan suatu persamaan?
  
pada awalnya kita hanya akan menuliskan untuk suatu persamaan dengan pangkat tertinggi yaitu . Dan tentu nantinya kita akan belajar untuk suatu persamaan yang mempunyai pangkat tertinggi . Persamaan dengan pangkat tertinggi disebut persamaan linear. Untuk menyelesaikan suatu persamaan linier, perhatikan masalah di bawah ini!
  

  
Tugas kita adalah mencari nilai yang memenuhi persamaan diatas. Semesta pembicaraan kita adalah seluruh bilangan real. Sebelum mencari nilai , kita perhatikan dulu hal-hal yang boleh dilakukan pada suatu persamaan atau kesamaan. Misalkan persamaan atau kesamaan tersebut berbentuk . yang boleh dilakukan yaitu :
  

1. Menambahkan atau mengurangi bilangan yang sama di ruas kanan dan ruas kiri. Untuk semua bilangan z, berlaku :
2. Mengalikan bilangan yang sama di ruas kanan dan ruas kiri. Untuk semua bilangan p berlaku :

  
Terkadang kita menyalah-artikan membagi ruas kanan dan ruas kiri dengan angka yang sama. Padahal ini artinya sama dengan point nomor 2, yaitu mengalikan dengan bilangan yang sama. Hanya saja pengalinya berbentuk pecahan. Konsep untuk membagi kedua ruas dengan bilangan yang sama itu adalah kurang aman. Karena tentu kita sudah tahu bahwa membagi dengan nol adalah hal yang tidak diperbolehkan di matematika. Sehingga untuk lebih amannya kita gunakan point 2. Yaitu mengalikan kedua ruas dengan , dengan n tidak sama dengan 0.
  
Kembali pada menyelesaikan suatu persamaan. Untuk menyelesaikan . Kita ikuti langkah-langkah berikut :
  
5x+7=2
5x+7–7=2–7  (kedua ruas dikurangi 7)
5x=–5
5x(1/5)=–5(1/5)  (kedua ruas dikalikan (1/5)
x=–1
  
Diperoleh nilai x yang memenuhi persamaan tersebut adalah -1. Ketika kita sudah sangat terbiasa dengan proses seperti ini. Kita bisa menganggap proses-proses seperti langkah pertama yaitu kedua ruas dikurangi 7. Kita bisa menganggap dengan memindahkan angka tujuh dari ruas kiri ke ruas kanan dan member tanda negative. Tentunya ketika pemindahan kita melewati tanda sama dengan, maka wajib bagi kita untuk merubah tanda. Yang semula positif menjadi negative. Dan yang semula negative menjadi positif.
 
Coba selesaikan persamaan-persamaan berikut :
 

1. 
2. 
3. 
4. 
5. 

 
 
Fungsi Linear
 
Fungsi linear adalah suatu fungsi yang mempunyai pangkat tertinggi yaitu 1. Misalnya  f(x)=5x, g(x)=2x+4, dll. Gambar grafik dari suatu fungsi linear merupakan garis lurus. Perhatikan gambar dibawah :
Gambar tersebut adalah gambar dari fungsi y=x–2. Gambarnya berupa garis lurus yang memotong sumbu x dan memotong sumbu y. Perhatikan bahwa gambar grafik tersebut memotong sumbu x di 2 dan memotong sumbu y di -2. Untuk menggambarkan suatu fungsi linear. Kita hanya perlu mencari 2 titik yang memenuhi persamaannya dan menarik garisnya. Misalnya gambar grafik dari  y=x–2 seperti gambar di atas. Kita masukkan nilai x (sebarang, asalkan tidak mempersulit kita dalam perhitungan). Untuk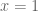 , maka nilai  y=1–2 atau  y=–1. Sehingga gambar grafiknya melewati koordinat (1, -1). Untuk x=0 diperoleh y=-2 yaitu koordinat (0, -2). Sehingga untuk menggambarkan grafik dari fungsi y=x–2 kita hanya perlu menarik garis lurus dari kedua titik tersebut.
Beberapa hal yang perlu diketahui pada suatu fungsi linear adalah :

1. Gambar dari suatu fungsi linear pasti merupakan suatu garis lurus.
2. Domain pada suatu fungsi linear adalah (-∞,∞).
3. Kemiringan grafik pada suatu fungsi linear adalah konstanta dari x. Misalnya y=2x. kemiringan dari grafik y=2x adalah 2. Ini dapat dicari menggunakan turunan pertama.
4. Dua garis yang mempunyai kemiringan sama, pasti kedua garis tersebut tidak akan pernah berpotongan.
5. Dua garis yang mempunyai kemiringan berbeda, pasti akan berpotongan.
6. Jika kemiringan dilambangkan m, maka dua garis tegak lurus jika m1*m₂=-1

Share this post