Akar 2, dituliskan dalam bentuk pecahan
Apa bisa?
Pertanyaan yang muncul pertama kali di kepala kita. Apa bisa 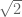 dituliskan ke dalam bentuk pecahan. Padahal selama ini kita mengenal
bentuk bilangan rasional saja yang bisa dituliskan ke dalam bentuk
pecahan.
dituliskan ke dalam bentuk pecahan. Padahal selama ini kita mengenal
bentuk bilangan rasional saja yang bisa dituliskan ke dalam bentuk
pecahan.
Memang, hanya bilangan rasional saja yang bisa dituliskan ke dalam bentuk pecahan dengan a dan b bilangan bulat dan b tidak sama dengan nol. Penulisan bilangan irasional ini ke dalam bentuk pecahan
dengan a dan b bilangan bulat dan b tidak sama dengan nol. Penulisan bilangan irasional ini ke dalam bentuk pecahan  tetapi b bukan merupakan bilangan bulat utuh.
tetapi b bukan merupakan bilangan bulat utuh.
Coba perhatikan bentuk berikut ini :
 Bentuk ini ternyata setara dengan
Bentuk ini ternyata setara dengan 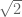 .
.
Dari mana ini berawal?
Perhatikan saja langkah-langkah berikut ini.
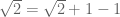

 …(2)
Kita perhatikan bentuk
…(2)
Kita perhatikan bentuk 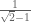 . Jika kita rasionalkan penyebutnya, maka kita dapatkan seperti berikut :
. Jika kita rasionalkan penyebutnya, maka kita dapatkan seperti berikut :

 Sehingga bentuk (2) bisa kita tuliskan menjadi,
Sehingga bentuk (2) bisa kita tuliskan menjadi,
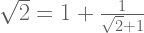 …(3)
Kemudian, bentuk
…(3)
Kemudian, bentuk 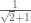 pada (3) bisa dituliskan menjadi
pada (3) bisa dituliskan menjadi
 Sehingga bentuk (3) bisa dituliskan menjadi,
Sehingga bentuk (3) bisa dituliskan menjadi,
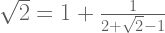 …(4)
Selanjutnya, bentuk
…(4)
Selanjutnya, bentuk 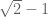 pada persamaan (4) kita ubah lagi sesuai langkah-langkah pada awal tadi. Sehingga bisa dituliskan menjadi,
pada persamaan (4) kita ubah lagi sesuai langkah-langkah pada awal tadi. Sehingga bisa dituliskan menjadi,
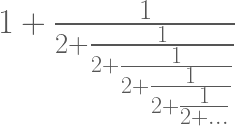
Memang, hanya bilangan rasional saja yang bisa dituliskan ke dalam bentuk pecahan
Coba perhatikan bentuk berikut ini :
Dari mana ini berawal?
Perhatikan saja langkah-langkah berikut ini.
0 Response to "Akar 2, dituliskan dalam bentuk pecahan"
Posting Komentar
Harap komentar yang bijak!!!