Akar pangkat n (untuk n mendekati tak hingga)

Berbicara mengenai bentuk akar, teringat dengan bilangan irasional. Karena bilangan irasional sangat erat hubungannya dengan bentuk akar. Lambang untuk akar sendiri yaitu $\sqrt{a}$ dengan a adalah sebarang bilangan. Jika a adalah bilangan negatif, maka bilangan akar tersebut masuk ke dalam bilangan kompleks. Sebenarnya apa bentuk akar itu?

$\sqrt{a}$ (baca: akar a). adalah suatu operasi yang sama dengan $a^{\frac{1}{2}}$ .

$\sqrt[n]{a}$

Bentuk tersebut sama dengan $a^{\frac{1}{n}}$ . Dengan n tidak boleh sama dengan nol. $\sqrt[n]{a}=b$ , artinya yaitu ada bilangan $b$ sedemikian sehingga, nilai berikut terpenuhi

$\underbrace{b \times b \times b \times \dots \times b \times b}_{n}=a$

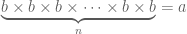
$\sqrt{a}$ lambang akar seperti itu adalah lambang yang digunakan untuk akar kuadrat. n di situ tidak
ditulis. Mungkin tujuannya untuk mempermudah penulisan, karena yang sering dipakai adalah akar kuadrat.

Lalu bagaimana dengan bentuk akar untuk n yang sangat besar?

Untuk nilai n yang sangat besar, dan nilai a tidak 0, maka bentuk akar akan menuju ke 1. Mengapa demikian? Perhaatikan bahwa bentuk akar itu sama dengan $a^{\frac{1}{n}}$ .
Untuk nilai n yang sangat besar, maka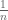 $\frac{1}{n}$ mendekati 0. Dan tentunya nilai dari $a^0$ untuk a tidak 0 adalah sama dengan 1. Jadi nilai akar untuk n yang sangat besar, apabila a tidak 0 atau pun negative, maka nilainya mendekati 1.

Bagaimana jika a = 0?

Untuk a = 0, tentunya dengan mudah kita menjawab bahwa nilainya sama dengan 0. Karena 0 dikalikan dengan sebarang bilangan hasilnya adalah 0. Begitu juga 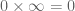$0 \times \infty =0$ .
Semoga bermanfaat.

Akar pangkat n (untuk n mendekati tak hingga)

0 Response to "Akar pangkat n (untuk n mendekati tak hingga)"

Posting Komentar

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel