Bilangan yang habis dibagi oleh a-b
Seringkali soal olimpiade dasar memunculkan soal habis dibagi. Beberapa soal-soalnya yaitu temukan sisa dari pembagian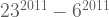 
dibagi dengan 
.
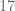Tentunya jika kita sudah mengetahui sifatnya, maka kita dengan mudah
bisa menjawabnya. Sisa hasil bagi itu adalah nol. Dengan kata lain, habis membagi 
Bagaimana kita menhitungnya? Bagaimana kita menunjukkannya?
Suatu sifat penting yang mudah untuk diingat (disarankan untuk mengingat, konsepnya saja tidak apa-apa). Bahwa, bilangan
selalu habis dibagi dengan 
. Bagaimana kita membuktikannya.
Sifat pemfaktoran pangkat yang sering kita lakukan. Bahwa
Ini juga berlaku untuk pangkat yang lebih besar dari 2
Untuk setiap n bilangan asli. Persamaan terakhir berlaku.
Jadi, adalah kelipatan dari . Ini akan memudahkan kita untuk membuktikan sutau bilangan apakah habis dibagi atau tidak. Jadi kesimpulannya, selalu habis dibagi dengan . Dengan n adalah bilangan asli.
Contoh soal :
Apakah
habis dibagi 
?
Tentu dengan mudah kita bisa menjawabnya. Karena
, maka habis dibagi
dibagi dengan .
Tentunya jika kita sudah mengetahui sifatnya, maka kita dengan mudah
bisa menjawabnya. Sisa hasil bagi itu adalah nol. Dengan kata lain, 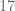habis membagi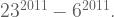 Bagaimana kita menhitungnya? Bagaimana kita menunjukkannya?
Suatu sifat penting yang mudah untuk diingat (disarankan untuk mengingat, konsepnya saja tidak apa-apa). Bahwa, bilangan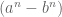
selalu habis dibagi dengan . Bagaimana kita membuktikannya.Sifat pemfaktoran pangkat yang sering kita lakukan. Bahwa
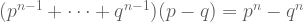
Untuk setiap n bilangan asli. Persamaan terakhir berlaku.
Jadi,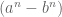
adalah kelipatan dari . Ini akan memudahkan kita untuk membuktikan sutau bilangan apakah habis dibagi atau tidak. Jadi kesimpulannya, 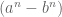selalu habis dibagi dengan . Dengan n adalah bilangan asli.Contoh soal :
Apakah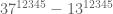
habis dibagi ?Tentu dengan mudah kita bisa menjawabnya. Karena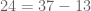
, maka 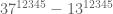habis dibagi 
0 Response to "Bilangan yang habis dibagi oleh a-b"
Posting Komentar
Harap komentar yang bijak!!!