Bukti teorema-teorema bilangan
Teorema. 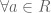 , berlaku
, berlaku  Bukti.
Bukti.
Menurut sifat identitas penjumlahan berlaku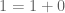 . Akibatnya,
. Akibatnya,  .
.
Jadi,
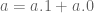 [sifat distributif]
[sifat distributif]
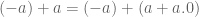
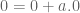
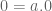
Teorema. Bilangan 0 tidak memiliki invers perkalian
Bukti.
Dari teorema di atas berlaku untuk setiap a. padahal bila 0 mempunyai invers berarti
untuk setiap a. padahal bila 0 mempunyai invers berarti 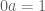 untuk suatu a, akibatnya
untuk suatu a, akibatnya  .
Hal ini tidak mungkin terjadi dalam bilangan real, sehingga haruslah
pernyataan 0 tidak mempunyai invers merupakan pernyataan yang benar.
.
Hal ini tidak mungkin terjadi dalam bilangan real, sehingga haruslah
pernyataan 0 tidak mempunyai invers merupakan pernyataan yang benar.
Teorema. Jika dan
dan 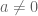 , maka
, maka 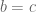
Bukti.
Diketahui dan
dan 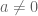 , artinya a mempunyai invers. Sehingga dapat dituliskan,
, artinya a mempunyai invers. Sehingga dapat dituliskan,
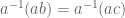

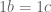
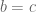
Teorema. dan
dan  , berlaku
, berlaku 
Bukti.
Kita tunjukkan bahwa adalah negative dari
adalah negative dari  , artinya
, artinya

Menurut hukum distributif,

Jadi,
Teorema. dan
dan  , berlaku
, berlaku 
Bukti.
Kita buktikan bahwa![[(-a) + (-b)] + (a + b) = 0 [(-a) + (-b)] + (a + b) = 0](https://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+0&bg=ffffff&fg=555555&s=0) seperti berikut,
seperti berikut,
![[(-a) + (-b)] + (a + b) = [(-a) + (-b)] + (a + b) [(-a) + (-b)] + (a + b) = [(-a) + (-b)] + (a + b)](https://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29&bg=ffffff&fg=555555&s=0)
![[(-a) + (-b)] + (a + b) = (-a) + (-b) + b + a [(-a) + (-b)] + (a + b) = (-a) + (-b) + b + a](https://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+%28-a%29+%2B+%28-b%29+%2B+b+%2B+a&bg=ffffff&fg=555555&s=0)
![[(-a) + (-b)] + (a + b) = (-a) + 0 + a [(-a) + (-b)] + (a + b) = (-a) + 0 + a](https://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+%28-a%29+%2B+0+%2B+a&bg=ffffff&fg=555555&s=0)
![[(-a) + (-b)] + (a + b) = (-a) + a [(-a) + (-b)] + (a + b) = (-a) + a](https://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+%28-a%29+%2B+a&bg=ffffff&fg=555555&s=0)
![[(-a) + (-b)] + (a + b) = 0 [(-a) + (-b)] + (a + b) = 0](https://s0.wp.com/latex.php?latex=%5B%28-a%29+%2B+%28-b%29%5D+%2B+%28a+%2B+b%29+%3D+0&bg=ffffff&fg=555555&s=0)
Teorema. jika dan hanya jika
jika dan hanya jika 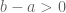
Bukti.
Jika , maka menurut sifat pada bilangan berlaku
, maka menurut sifat pada bilangan berlaku  . oleh karena itu didapatkan
. oleh karena itu didapatkan 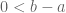 . yang tidak lain yaitu
. yang tidak lain yaitu 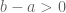 . Sebaliknya, jika
. Sebaliknya, jika 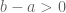 , maka
, maka 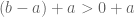 . dan diperoleh
. dan diperoleh 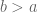
Teorema. dan
dan  , maka
, maka 
Bukti.
Jika , maka
, maka 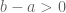 . Akibatnya, menurut sifat pada bilangan didapatkan
. Akibatnya, menurut sifat pada bilangan didapatkan  . sama dengan
. sama dengan  . Sehingga
. Sehingga  . Jadi menurut teorema sebelumnya, diperoleh
. Jadi menurut teorema sebelumnya, diperoleh 
Teorema. Jika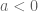 , maka
, maka 
Bukti.
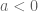 maka
maka 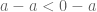 . diperoleh
. diperoleh 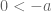 . Sama dengan
. Sama dengan 
Teorema. Jika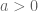 , maka
, maka 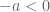
Bukti.
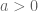 maka
maka  . diperoleh
. diperoleh 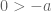 . Sama dengan
. Sama dengan 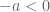
Teorema. dan
dan 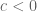 , maka
, maka 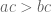
Bukti.
Jika , maka
, maka 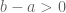 . Padahal
. Padahal 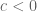 . Maka
. Maka  . maka
. maka 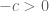 . Akibatnya didapatkan
. Akibatnya didapatkan 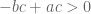 . Jadi menurut teorema sebelumnya, diperoleh
. Jadi menurut teorema sebelumnya, diperoleh 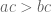
Menurut sifat identitas penjumlahan berlaku
Jadi,
Teorema. Bilangan 0 tidak memiliki invers perkalian
Bukti.
Dari teorema di atas berlaku
Teorema. Jika
Bukti.
Diketahui
Teorema.
Bukti.
Kita tunjukkan bahwa
Menurut hukum distributif,
Jadi,
Teorema.
Bukti.
Kita buktikan bahwa
Teorema.
Bukti.
Jika
Teorema.
Bukti.
Jika
Teorema. Jika
Bukti.
Teorema. Jika
Bukti.
Teorema.
Bukti.
Jika
0 Response to "Bukti teorema-teorema bilangan"
Posting Komentar
Harap komentar yang bijak!!!