Tidak semua bilangan ganjil bisa dituliskan
Sebenarnya, judul lengkapnya adalah tidak semua bilangan ganjil yang
lebih besar dari 1 dapat dituliskan sebagai 2 pangkat n ditambah
bilangan prima, dengan n adalah bilangan cacah tentunya. Perhatikan saja
berikut ini.
Misalnya saja kita ingin menulis bilangan ganjil dalam bentuk seperti itu.
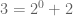
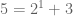
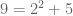
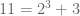
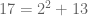
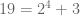
Ternyata ditemukan suatu bilangan ganjil yang tidak bisa dituliskan ke dalam bentuk yang dimaksud. Bilangan tersebut adalah 127. Sebagaimana jika kita mencoba menuliskannya dengan menggunakan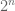
. Dengan n adalah bilangan cacah yang urut dan dimulai dari 0.
Percobaannya adalah sebagai berikut ini :
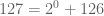
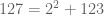
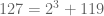
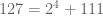
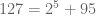
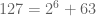
Bilangan-bilangan 126, 125, 123, 119, 111, 95 dan 63 ternyata bukan merupakan bilangan prima. Sehingga ini menggagalkan suatu gagasan bahwa setiap bilangan ganjil bisa dituliskan ke dalam bentuk bilangan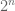 (dengan n bilangan cacah) ditambah dengan bilangan prima.
Usaha memang harus diberikan suatu acungan jempol.
Misalnya saja kita ingin menulis bilangan ganjil dalam bentuk seperti itu.
Ternyata ditemukan suatu bilangan ganjil yang tidak bisa dituliskan ke dalam bentuk yang dimaksud. Bilangan tersebut adalah 127. Sebagaimana jika kita mencoba menuliskannya dengan menggunakan
. Dengan n adalah bilangan cacah yang urut dan dimulai dari 0.Percobaannya adalah sebagai berikut ini :
Bilangan-bilangan 126, 125, 123, 119, 111, 95 dan 63 ternyata bukan merupakan bilangan prima. Sehingga ini menggagalkan suatu gagasan bahwa setiap bilangan ganjil bisa dituliskan ke dalam bentuk bilangan
(dengan n bilangan cacah) ditambah dengan bilangan prima.Usaha memang harus diberikan suatu acungan jempol.
0 Response to "Tidak semua bilangan ganjil bisa dituliskan"
Posting Komentar
Harap komentar yang bijak!!!