Fungsi bilangan bulat terbesar
Fungsi bilangan bulat terbesar disimbolkan dengan ![\big[ | \, \, | \big] \big[ | \, \, | \big]](https://s0.wp.com/latex.php?latex=%5Cbig%5B+%7C+%5C%2C+%5C%2C+%7C+%5Cbig%5D&bg=ffffff&fg=555555&s=0) Definisinya adalah :
Definisinya adalah : ![\big[ |x| \big] \big[ |x| \big]](https://s0.wp.com/latex.php?latex=%5Cbig%5B+%7Cx%7C+%5Cbig%5D&bg=ffffff&fg=555555&s=0) adalah bilangan bulat yang lebih kecil atau sama dengan x
adalah bilangan bulat yang lebih kecil atau sama dengan x
Misalnya![\big[ |3,2| \big]=3 \big[ |3,2| \big]=3](https://s0.wp.com/latex.php?latex=%5Cbig%5B+%7C3%2C2%7C+%5Cbig%5D%3D3&bg=ffffff&fg=555555&s=0) ,
, ![\big[ |4| \big]=4 \big[ |4| \big]=4](https://s0.wp.com/latex.php?latex=%5Cbig%5B+%7C4%7C+%5Cbig%5D%3D4&bg=ffffff&fg=555555&s=0)
,![\big[ |5,99| \big]=5 \big[ |5,99| \big]=5](https://s0.wp.com/latex.php?latex=%5Cbig%5B+%7C5%2C99%7C+%5Cbig%5D%3D5&bg=ffffff&fg=555555&s=0) , dan seterusnya.. .
, dan seterusnya.. .
Contoh yang negatif,![\big[ |-2,5| \big]=-3 \big[ |-2,5| \big]=-3](https://s0.wp.com/latex.php?latex=%5Cbig%5B+%7C-2%2C5%7C+%5Cbig%5D%3D-3&bg=ffffff&fg=555555&s=0)
Bagaimana penggambaran grafiknya?
Contoh grafiknya yang sederhana adalah fungsi bilangan bulat terbesar![y= \big[ |x| \big] y= \big[ |x| \big]](https://s0.wp.com/latex.php?latex=y%3D+%5Cbig%5B+%7Cx%7C+%5Cbig%5D&bg=ffffff&fg=555555&s=0)
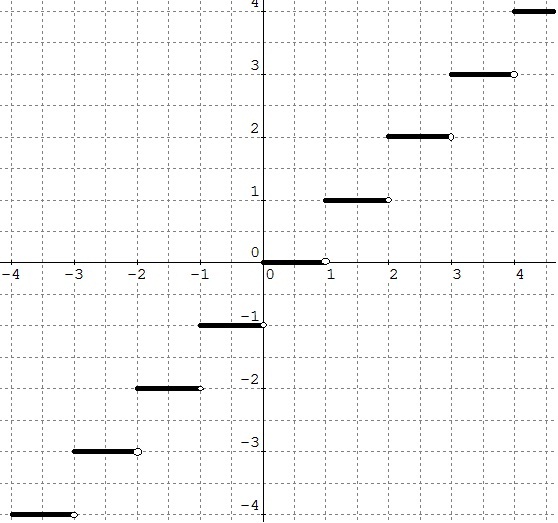
Beberapa sifat sederhana untuk![y= \big[ |x| \big] y= \big[ |x| \big]](https://s0.wp.com/latex.php?latex=y%3D+%5Cbig%5B+%7Cx%7C+%5Cbig%5D&bg=ffffff&fg=555555&s=0)
*Jelas tidak kontinu.. . Limit kanan tidak sama dengan limit kiri. Ambil saja untuk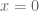 , maka limit dari arah kanan sama dengan nol, sedangkan limit dari arah kiri sama dengan -1.
, maka limit dari arah kanan sama dengan nol, sedangkan limit dari arah kiri sama dengan -1.
Bukan hanya untuk x=0, tetapi untuk x anggota bilangan bulat yang lain juga tidak kontinu.
*Bukan merupakan fungsi genap, bukan juga merupakan fungsi ganjil. Karena tidak berlaku sifat-sifat fungsi ganjil, dan juga fungsi genap.
Dilihat dari grafiknya juga jelas kelihatan.
*![y= \big[ |x+a| \big] y= \big[ |x+a| \big]](https://s0.wp.com/latex.php?latex=y%3D+%5Cbig%5B+%7Cx%2Ba%7C+%5Cbig%5D&bg=ffffff&fg=555555&s=0) tidak selalu sama dengan
tidak selalu sama dengan ![y= \big[ |x| \big]+a y= \big[ |x| \big]+a](https://s0.wp.com/latex.php?latex=y%3D+%5Cbig%5B+%7Cx%7C+%5Cbig%5D%2Ba&bg=ffffff&fg=555555&s=0)
Ambil a bukan bilangan bulat, misal a=0,5 , dan ambil x=1, maka
![\big[ |1+0,5| \big]=1 \ne \big[ |1| \big]+0,5 = 1,5 \big[ |1+0,5| \big]=1 \ne \big[ |1| \big]+0,5 = 1,5](https://s0.wp.com/latex.php?latex=%5Cbig%5B+%7C1%2B0%2C5%7C+%5Cbig%5D%3D1+%5Cne+%5Cbig%5B+%7C1%7C+%5Cbig%5D%2B0%2C5+%3D+1%2C5&bg=ffffff&fg=555555&s=0)
Disebut lain sebagai fungsi tangga. Karena gambar grafiknya mirip dengan bentuk tangga.
Bagaimana pembaca menggambarkan fungsi tangga berikut ini :
![y= \big[ |x+2| \big] y= \big[ |x+2| \big]](https://s0.wp.com/latex.php?latex=y%3D+%5Cbig%5B+%7Cx%2B2%7C+%5Cbig%5D&bg=ffffff&fg=555555&s=0)
![y= \big[ |2x| \big] y= \big[ |2x| \big]](https://s0.wp.com/latex.php?latex=y%3D+%5Cbig%5B+%7C2x%7C+%5Cbig%5D&bg=ffffff&fg=555555&s=0)
![y= \big[ |x/2| \big] y= \big[ |x/2| \big]](https://s0.wp.com/latex.php?latex=y%3D+%5Cbig%5B+%7Cx%2F2%7C+%5Cbig%5D&bg=ffffff&fg=555555&s=0)
Misalnya
,
Contoh yang negatif,
Bagaimana penggambaran grafiknya?
Contoh grafiknya yang sederhana adalah fungsi bilangan bulat terbesar

Beberapa sifat sederhana untuk
*Jelas tidak kontinu.. . Limit kanan tidak sama dengan limit kiri. Ambil saja untuk
Bukan hanya untuk x=0, tetapi untuk x anggota bilangan bulat yang lain juga tidak kontinu.
*Bukan merupakan fungsi genap, bukan juga merupakan fungsi ganjil. Karena tidak berlaku sifat-sifat fungsi ganjil, dan juga fungsi genap.
Dilihat dari grafiknya juga jelas kelihatan.
*
Ambil a bukan bilangan bulat, misal a=0,5 , dan ambil x=1, maka
Disebut lain sebagai fungsi tangga. Karena gambar grafiknya mirip dengan bentuk tangga.
Bagaimana pembaca menggambarkan fungsi tangga berikut ini :
0 Response to "Fungsi bilangan bulat terbesar"
Posting Komentar
Harap komentar yang bijak!!!