Ciri bilangan habis dibagi 2, 3, 4, 5, 6, 7, 8 atau 9
Syarat atau ciri bilangan yang habis dibagi 2
Suatu bilangan habis dibagi 2 apabila bilangan tersebut berakhiran (berangka satuan) 0, 2, 4, 6, atau 8. Dengan kata lain bilangan itu adalah bilangan genap.
Contoh : Apakah 74 habis dibagi 2? Karena 74 merupakan bilangan genap (Ingat rumus untuk bilangan genap. Rumus untuk bilangan genap adalah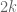 untuk sebarang
untuk sebarang  bilangan bulat. Sedangkan untuk bilangan ganjil yaitu
bilangan bulat. Sedangkan untuk bilangan ganjil yaitu  untuk sebarang
untuk sebarang  bilangan bulat). Karena 74 memenuhi rumus bilangan genap, maka 74 habis dibagi 2.
bilangan bulat). Karena 74 memenuhi rumus bilangan genap, maka 74 habis dibagi 2.
Bukti :
Untuk sebarang bilangan misalnya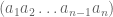 sebanyak
sebanyak 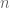 digit. Bentuk tersebut dapat kita tuliskan menjadi bentuk
digit. Bentuk tersebut dapat kita tuliskan menjadi bentuk

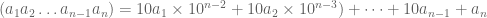
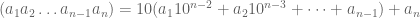
Karena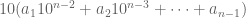 habis dibagi
habis dibagi  , maka agar bilangan habis dibagi
, maka agar bilangan habis dibagi  harusnya
harusnya  habis dibagi
habis dibagi  . Dimana
. Dimana  adalah digit terakhir (satuan) dari angka kita. Sehingga ciri bilangan habis dibagi
adalah digit terakhir (satuan) dari angka kita. Sehingga ciri bilangan habis dibagi  yaitu digit terakhirnya (satuannya) habis dibagi
yaitu digit terakhirnya (satuannya) habis dibagi  . Yaitu
. Yaitu 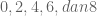 . Yang tidak lain merupakan bilangan genap.
. Yang tidak lain merupakan bilangan genap.
Syarat atau ciri bilangan yang habis dibagi 3
Jumlah digit-digitnya habis dibagi 3
Contoh : Apakah 213 habis dibagi 3? Akan kita jumlahkan digit-digit pada bilangan 213. Didapatkan,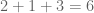 . Karena
. Karena  (hasil dari penjumlahan digit-digitnya) habis dibagi
(hasil dari penjumlahan digit-digitnya) habis dibagi  . Maka bilangan itu
. Maka bilangan itu 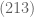 habis dibagi
habis dibagi  .
.
Bukti :
Untuk sebarang bilangan misalnya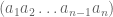 sebanyak
sebanyak 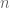 digit. Bentuk tersebut dapat kita tuliskan menjadi bentuk
digit. Bentuk tersebut dapat kita tuliskan menjadi bentuk

Sekarang perhatikan ini
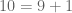
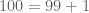
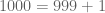

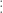
 pada bilangan
pada bilangan  sebanyak
sebanyak 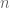 angka
angka 
Kemudian perhatikan ini



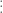

perhatikan bahwa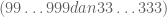 jumlah digitnya sebanyak
jumlah digitnya sebanyak 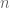
Dari situ kita dapatkan :
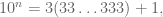
 jumlah digitnya sebanyak
jumlah digitnya sebanyak 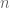
Disini kita akan menuliskan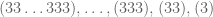 sebagai lambang
sebagai lambang 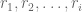 . Ingat bahwa
. Ingat bahwa  adalah kelipatan
adalah kelipatan 
Sehingga kita bisa menulis :



Karena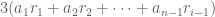 habis dibagi
habis dibagi  . Maka agar
. Maka agar 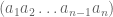 habis dibagi
habis dibagi  . Harusnya
. Harusnya  habis dibagi
habis dibagi  . Dimana
. Dimana 
adalah jumlah angka-angkanya (jumlah digit-digitnya). Sehingga syarat bilangan habis dibagi adalah jumlah digit-digitnya harus habis dibagi
adalah jumlah digit-digitnya harus habis dibagi 
Syarat atau ciri bilangan yang habis dibagi 4
Dua digit terakhir habis dibagi 4. Lebih mudahnya yaitu puluhan dari bilangan itu habis dibagi 4.
Contoh : Apakah 324 habis dibagi 4? Dua digit terakhir yaitu 24. Dan 24 habis dibagi 4. Sehingga 326 habis dibagi 4. Apakah 2006 habis dibagi 4? Tidak. Karena dua angka terahirnya yaitu 06. Sedangkan 06 tidak habis dibagi 4. Sehingga 2006 tidak habis dibagi 4.
Bukti ditinggalkan sebagai latihan. Tips untuk membuktikan, langkah yang digunakan hampir sama dengan pembuktian bilangan habis dibagi dua. Hanya saja nantinya memakai angka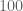 . Karena
. Karena 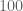 habis dibagi
habis dibagi 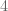 , sedangkan
, sedangkan 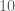 tidak habis dibagi
tidak habis dibagi 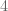 .
.
Syarat atau ciri bilangan yang habis dibagi 5
Bilangan tersebut berakhiran 0 atau 5.
Contoh : Apakah 3255 habis dibagi 5? Digit terakhir adalah 5. Sehingga 3255 habis dibagi 5. Apakah 2005 habis dibagi 5? Sangatlah mudah menentukan ciri bilangan habis dibagi 5.
Buktinya sama dengan pembuktian pada ciri bilangan yang habis dibagi .
.
Syarat atau ciri bilangan yang habis dibagi
Ciri bilangan yang habis dibagi adalah bilangan genap yang jumlah angka-angkanya habis dibagi
adalah bilangan genap yang jumlah angka-angkanya habis dibagi  . Atau bilangan yang habis dibagi
. Atau bilangan yang habis dibagi  dan habis dibagi
dan habis dibagi  .
.
Contoh : apakah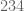 habis dibagi 6? Sekarang kita perhatikan jumlah angka-angkanya.
habis dibagi 6? Sekarang kita perhatikan jumlah angka-angkanya.  . Dan
. Dan  habis dibagi
habis dibagi  . Karena jumlah angka-angkanya habis dibagi
. Karena jumlah angka-angkanya habis dibagi  dan bilangan itu genap. Maka
dan bilangan itu genap. Maka 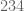 habis dibagi
habis dibagi  .
.
Bukti :
Kita juga bisa mengatakan bahwa jika bilangan habis dibagi , maka bilangan itu habis dibagi
, maka bilangan itu habis dibagi  dan habis dibagi
dan habis dibagi  .
.
Bukti :
Misalkan bilangan itu .
.

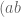 membagi
membagi 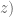 atau
atau  . menurut definisi, ada
. menurut definisi, ada  bilangan bulat sehingga
bilangan bulat sehingga 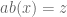 .
.
Didapatkan dan
dan  . Sehingga diperoleh
. Sehingga diperoleh  dan
dan  . Karena
. Karena  . Sehingga syarat bilangan habis dibagi
. Sehingga syarat bilangan habis dibagi  . Harus memenuhi syarat bilangan habis dibagi
. Harus memenuhi syarat bilangan habis dibagi  dan syarat bilangan habis dibagi
dan syarat bilangan habis dibagi  . Dengan kata lain, syarat bilangan habis dibagi
. Dengan kata lain, syarat bilangan habis dibagi  adalah apabila digit-digitnya dijumlahkan harus habis dibagi
adalah apabila digit-digitnya dijumlahkan harus habis dibagi  dan angkanya berakhiran
dan angkanya berakhiran 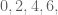 dan
dan 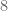 . Atau bisa dikatakan bilangan habis dibagi
. Atau bisa dikatakan bilangan habis dibagi  adalah bilangan genap yang apabila digit-digitnya dijumlahkan maka habis dibagi
adalah bilangan genap yang apabila digit-digitnya dijumlahkan maka habis dibagi 
Syarat atau ciri bilangan yang habis dibagi 7
Bila bagian satuannya dikalikan , dan menjadi pengurang dari bilangan tersisa. Jika hasilnya habis dibagi
, dan menjadi pengurang dari bilangan tersisa. Jika hasilnya habis dibagi 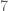 , maka bilangan itu habis dibagi
, maka bilangan itu habis dibagi 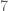 .
.
Contoh : apakah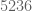 habis dibagi 7? Kita pisahkan
habis dibagi 7? Kita pisahkan  (satuannya), kemudian
(satuannya), kemudian 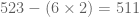 . Apakah
. Apakah 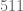 habis dibagi 7?
habis dibagi 7?  . Karena
. Karena 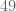 habis dibagi
habis dibagi 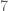 , maka
, maka 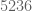 habis dibagi
habis dibagi 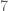 .
.
Bukti :
Misalkan bilangan awal adalah P
 sebanyak
sebanyak 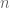 digit. Ini adalah bilangan awal.
digit. Ini adalah bilangan awal.
 bedakan dengan yang di atas. Yang ini berkurang satu digit.
bedakan dengan yang di atas. Yang ini berkurang satu digit.
Sehingga diperoleh hubungan antara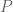 dan
dan 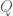 , yaitu
, yaitu 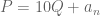 .
.
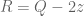 ini adalah syarat bilangan habis dibagi 7.
ini adalah syarat bilangan habis dibagi 7.
Kita dapat menuliskan syarat bilangan habis dibagi 7 seperti ini : Jika bilangan habis dibagi 7 maka (perhatikan di atas)
di atas)  habis dibagi 7. Jika
habis dibagi 7. Jika  habis dibagi 7 maka bilangan awal habis dibagi 7. Dari pernyataan itu
bisa dikatakan : “bilangan habis dibagi 7 jika dan hanya jika
habis dibagi 7 maka bilangan awal habis dibagi 7. Dari pernyataan itu
bisa dikatakan : “bilangan habis dibagi 7 jika dan hanya jika  habis dibagi 7.” Sehingga kita harus membuktikan dua kali. yaitu untuk Jika bilangan habis dibagi 7 maka
habis dibagi 7.” Sehingga kita harus membuktikan dua kali. yaitu untuk Jika bilangan habis dibagi 7 maka  habis dibagi 7. Dan untuk jika
habis dibagi 7. Dan untuk jika  habis dibagi 7 maka bilangan awal habis dibagi 7.
habis dibagi 7 maka bilangan awal habis dibagi 7.
Bukti untuk Jika bilangan habis dibagi 7 maka habis dibagi 7
habis dibagi 7
Bilangan awal yaitu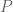 . dan diketahui
. dan diketahui 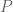 habis dibagi 7.
habis dibagi 7.
Kita tulis (lambang
(lambang 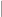 adalah sebuah garis vertical pada keterbagian. Contohnya
adalah sebuah garis vertical pada keterbagian. Contohnya  . Yang artinya
. Yang artinya  habis dibagi
habis dibagi  . atau
. atau  adalah factor dari
adalah factor dari  )
)


Kita punya teorema, jika , maka
, maka 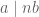 dengan
dengan 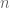 bilangan bulat. Sehingga kita boleh menuliskan
bilangan bulat. Sehingga kita boleh menuliskan
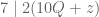
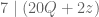
Sekarang perhatikan bahwa 21 habis dibagi 7. Tentunya kelipatan dari 21 juga habis dibagi 7.


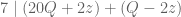
Dalam keterbagian, kita punya teorema jika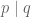 dan
dan  maka
maka 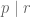
Sehingga diperoleh
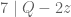
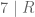
Terbukti
Bukti untuk jika habis dibagi 7 maka bilangan awal habis dibagi 7.
habis dibagi 7 maka bilangan awal habis dibagi 7.
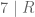
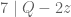
Menurut teorema, jika , maka
, maka 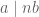 dengan
dengan 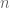 bilangan bulat.
bilangan bulat.


Seperti halnya bukti yang pertama, 21 habis dibagi 7. Sehingga,



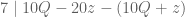
Ada teorema pada keterbagian yang mengatakan, jika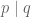 dan
dan  maka
maka 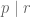
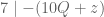
Menurut teorema, jika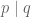 maka
maka 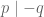 . Maka,
. Maka,


Terbukti
Bilangan habis dibagi 8
Tiga digit terakhir habis dibagi 8.
Contoh : apakah 2168 habis dibagi 8. Iya, karena 168 habis dibagi 8.
Buktinya diserahkan kepada pembaca. Tipsnya, gunakan langkah yang mirip dengan ciri bilangan habis dibagi 2 dan 4. Nantinya akan ditemukan suatu hal yang menarik bahwa ciri bilangan habis dibagi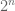 akan ada hubungannya dengan
akan ada hubungannya dengan 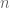 digit terakhirnya
digit terakhirnya
Bilangan yang habis dibagi 9
Jumlah angka-angkanya habis dibagi 9.
Contoh : apakah 819 habis dibagi 9? Jumlah digit-digitnya yaitu 8 + 1 + 9 = 18. Dan 18 habis dibagi 9. Sehingga 819 habis dibagi 9.
Bukti : sama dengan ciri bilangan habis dibagi 3. Coba selesaikan…
Suatu bilangan habis dibagi 2 apabila bilangan tersebut berakhiran (berangka satuan) 0, 2, 4, 6, atau 8. Dengan kata lain bilangan itu adalah bilangan genap.
Contoh : Apakah 74 habis dibagi 2? Karena 74 merupakan bilangan genap (Ingat rumus untuk bilangan genap. Rumus untuk bilangan genap adalah
Bukti :
Untuk sebarang bilangan misalnya
Karena
Syarat atau ciri bilangan yang habis dibagi 3
Jumlah digit-digitnya habis dibagi 3
Contoh : Apakah 213 habis dibagi 3? Akan kita jumlahkan digit-digit pada bilangan 213. Didapatkan,
Bukti :
Untuk sebarang bilangan misalnya
Sekarang perhatikan ini
Kemudian perhatikan ini
perhatikan bahwa
Dari situ kita dapatkan :
Disini kita akan menuliskan
Sehingga kita bisa menulis :
Karena
adalah jumlah angka-angkanya (jumlah digit-digitnya). Sehingga syarat bilangan habis dibagi
Syarat atau ciri bilangan yang habis dibagi 4
Dua digit terakhir habis dibagi 4. Lebih mudahnya yaitu puluhan dari bilangan itu habis dibagi 4.
Contoh : Apakah 324 habis dibagi 4? Dua digit terakhir yaitu 24. Dan 24 habis dibagi 4. Sehingga 326 habis dibagi 4. Apakah 2006 habis dibagi 4? Tidak. Karena dua angka terahirnya yaitu 06. Sedangkan 06 tidak habis dibagi 4. Sehingga 2006 tidak habis dibagi 4.
Bukti ditinggalkan sebagai latihan. Tips untuk membuktikan, langkah yang digunakan hampir sama dengan pembuktian bilangan habis dibagi dua. Hanya saja nantinya memakai angka
Syarat atau ciri bilangan yang habis dibagi 5
Bilangan tersebut berakhiran 0 atau 5.
Contoh : Apakah 3255 habis dibagi 5? Digit terakhir adalah 5. Sehingga 3255 habis dibagi 5. Apakah 2005 habis dibagi 5? Sangatlah mudah menentukan ciri bilangan habis dibagi 5.
Buktinya sama dengan pembuktian pada ciri bilangan yang habis dibagi
Syarat atau ciri bilangan yang habis dibagi
Ciri bilangan yang habis dibagi
Contoh : apakah
Bukti :
Kita juga bisa mengatakan bahwa jika bilangan habis dibagi
Bukti :
Misalkan bilangan itu
Didapatkan
Syarat atau ciri bilangan yang habis dibagi 7
Bila bagian satuannya dikalikan
Contoh : apakah
Bukti :
Misalkan bilangan awal adalah P
Sehingga diperoleh hubungan antara
Kita dapat menuliskan syarat bilangan habis dibagi 7 seperti ini : Jika bilangan habis dibagi 7 maka (perhatikan
Bukti untuk Jika bilangan habis dibagi 7 maka
Bilangan awal yaitu
Kita tulis
Kita punya teorema, jika
Sekarang perhatikan bahwa 21 habis dibagi 7. Tentunya kelipatan dari 21 juga habis dibagi 7.
Dalam keterbagian, kita punya teorema jika
Sehingga diperoleh
Terbukti
Bukti untuk jika
Menurut teorema, jika
Seperti halnya bukti yang pertama, 21 habis dibagi 7. Sehingga,
Ada teorema pada keterbagian yang mengatakan, jika
Menurut teorema, jika
Terbukti
Bilangan habis dibagi 8
Tiga digit terakhir habis dibagi 8.
Contoh : apakah 2168 habis dibagi 8. Iya, karena 168 habis dibagi 8.
Buktinya diserahkan kepada pembaca. Tipsnya, gunakan langkah yang mirip dengan ciri bilangan habis dibagi 2 dan 4. Nantinya akan ditemukan suatu hal yang menarik bahwa ciri bilangan habis dibagi
Bilangan yang habis dibagi 9
Jumlah angka-angkanya habis dibagi 9.
Contoh : apakah 819 habis dibagi 9? Jumlah digit-digitnya yaitu 8 + 1 + 9 = 18. Dan 18 habis dibagi 9. Sehingga 819 habis dibagi 9.
Bukti : sama dengan ciri bilangan habis dibagi 3. Coba selesaikan…
0 Response to "Ciri bilangan habis dibagi 2, 3, 4, 5, 6, 7, 8 atau 9"
Posting Komentar
Harap komentar yang bijak!!!