Bilangan irasional yang nilainya mendekati bilangan bulat
Suatu ketika saya mencoba untuk melihat blog-blog tentang sains
(khusunya matematika). Saya menemukan sebuah blog berbahasa spanyol.
Bahasa yang sangat asing bagi saya. Tetapi di dalamnya ada tulisan yang
sangat menarik perhatian saya. Mengenai bilangan irasional yang nilainya
mendekati bilangan bulat. Saya pun langsung menerjemahkan blog dalam
bahasa spanyol tersebut ke dalam bahasa indonesia.
Di dalamnya banyak bentuk bilangan irasional yang nilainya mendekati bilangan bulat. Yang paling saya ingat yaitu
dalam radian (bukan 
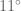). Nilainya hampir mendekati 
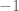. Dengan angka 
berulang lima kali setelah tanda koma. Beberapa hal yang lain yaitu melibatkan bilangan rasional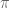 
(pi), 
(phi) dan 
Angka
berulang lima kali setelah tanda koma.
Berikut ini adalah bilangan-bilangan irasional yang lainnya
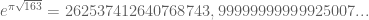
Angka berulang 
kali. Bilangan tersebut sedikit diubah
![\frac{\sqrt[3]{e^\pi \sqrt{163}-744}}{10}=64031,99999999999999999999999993903...](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%5Csqrt%5B3%5D%7Be%5E%5Cpi+%5Csqrt%7B163%7D-744%7D%7D%7B10%7D%3D64031%2C99999999999999999999999993903...&bg=ffffff&fg=555555&s=2 "\frac{\sqrt[3]{e^\pi \sqrt{163}-744}}{10}=64031,99999999999999999999999993903...")
Angka berulang sebanyak 
kali. Diubah lagi, untuk mendapatkan yang hampir mendekati seperti berikut
![\frac{\sqrt[3]{e^\pi \sqrt{163}-744}}{5280} - 30303 \sqrt{61}= 236673,99999999999999999999999999999999999999999999987253...](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%5Csqrt%5B3%5D%7Be%5E%5Cpi+%5Csqrt%7B163%7D-744%7D%7D%7B5280%7D+-+30303+%5Csqrt%7B61%7D%3D+236673%2C99999999999999999999999999999999999999999999987253...+&bg=ffffff&fg=555555&s=0 "\frac{\sqrt[3]{e^\pi \sqrt{163}-744}}{5280} - 30303 \sqrt{61}= 236673,99999999999999999999999999999999999999999999987253...")
Angka berulang sampai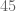 
kali. angka yang sangat dekat dengan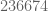 
Karena hal tersebut saya mencoba mengutak-atik bilangan irasional. Dengan menggunakan komputer, saya mencoba mencari bilangan irasional yang hasilnya hampir bilangan bulat. Tidak sia-sia, hasil yang saya dapatkan sebagai berikut :
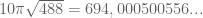
Angka berulang tiga kali, bilangan tersebut hampir sama dengan bilangan 
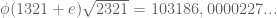
Bilangan-bilangan selanjutnya dengan angka berulang lima kali
Berikut angka berulang enam kali dan tujuh kali
Bilangan-bilangan yang tidak terduga. Meskipun hasilnya masih paling banyak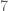
angka berulang di belakang koma, tetapi hasilnya memuaskan bagi saya pribadi.
Semoga tulisan ini bermanfaat untuk pembaca.
bisa juga dibaca di sini
msihabudin
Di dalamnya banyak bentuk bilangan irasional yang nilainya mendekati bilangan bulat. Yang paling saya ingat yaitu
dalam radian (bukan ). Nilainya hampir mendekati . Dengan angka berulang lima kali setelah tanda koma. Beberapa hal yang lain yaitu melibatkan bilangan rasional (pi), (phi) dan Angka
berulang lima kali setelah tanda koma.Berikut ini adalah bilangan-bilangan irasional yang lainnya
Angka
berulang kali. Bilangan tersebut sedikit diubahAngka
berulang sebanyak kali. Diubah lagi, untuk mendapatkan yang hampir mendekati seperti berikutAngka
berulang sampai kali. angka yang sangat dekat dengan Karena hal tersebut saya mencoba mengutak-atik bilangan irasional. Dengan menggunakan komputer, saya mencoba mencari bilangan irasional yang hasilnya hampir bilangan bulat. Tidak sia-sia, hasil yang saya dapatkan sebagai berikut :
Angka
berulang tiga kali, bilangan tersebut hampir sama dengan bilangan Bilangan-bilangan selanjutnya dengan angka
berulang lima kaliBerikut angka
berulang enam kali dan tujuh kaliBilangan-bilangan yang tidak terduga. Meskipun hasilnya masih paling banyak
angka berulang di belakang koma, tetapi hasilnya memuaskan bagi saya pribadi.Semoga tulisan ini bermanfaat untuk pembaca.
bisa juga dibaca di sini
msihabudin
0 Response to "Bilangan irasional yang nilainya mendekati bilangan bulat"
Posting Komentar
Harap komentar yang bijak!!!