Bukti bahwa akar dua adalah bilangan irasional
Akar dua merupakan bilangan irasional. Kita akan menunjukkan dengan menggunakan kontradiksi. Bahwa akar dua irasional.
Untuk menunjukkan dengan kontradiksi maka kita asumsikan bahwa
Pernyataan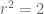
Pernyataan kesimpulan salah, yang benar r bilangan rasional
Oleh karena itu, berdasarkan asumsi bahwa r adalah bilangan rasional. Maka r dapat dituliskan menjadi bentuk
dengan p dan q merupakan bilangan bulat yang pembagi bersama terbesar adalah 1. Serta memenuhi
karena ruas kanan merupakan bilangan genap. Maka ruas kiri juga
merupakan bilangan genap. Dengan demikian p juga merupakan bilangan
genap.
Tuliskan
dengan k adalah suatu bilangan bulat yang lain.
Maka diperoleh
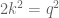
Akibatnya ruas kanan juga merupakan bilangan genap. Maka q juga genap.
Kesimpulannya p dan q merupakan bilangan genap.
Hal ini kontradiksi dengan anggapan bahwa pembagi bersama terbesar dari p dan q adalah 1.
Ini membuktikan bahwa akar 2 merupakan bilangan irasional.
Bukti akar 2 adalah bilangan irasional sudah terbukti.
Semoga bermanfaat.
Pernyataan
Pernyataan kesimpulan salah, yang benar r bilangan rasional
Oleh karena itu, berdasarkan asumsi bahwa r adalah bilangan rasional. Maka r dapat dituliskan menjadi bentuk
dengan p dan q merupakan bilangan bulat yang pembagi bersama terbesar adalah 1. Serta memenuhi Tuliskan
dengan k adalah suatu bilangan bulat yang lain.Maka diperoleh
Kesimpulannya p dan q merupakan bilangan genap.
Hal ini kontradiksi dengan anggapan bahwa pembagi bersama terbesar dari p dan q adalah 1.
Ini membuktikan bahwa akar 2 merupakan bilangan irasional.
Bukti akar 2 adalah bilangan irasional sudah terbukti.
Semoga bermanfaat.
0 Response to "Bukti bahwa akar dua adalah bilangan irasional"
Posting Komentar
Harap komentar yang bijak!!!