Semua Tentang Bilangan Prima

Papercut Handmade
Sebagai hadiah ulang tahun, hadian pernikahan, dll
Cocok diberikan kepada pasangan, sahabat, anak, atau untuk hiasan rumah.

Contact :
Harga dan Informasi
WA/Line : 085230646886
BBM : 59423DB0

Bilangan Prima

Siapa yang tidak mengenal Bilangan Prima?
Sejak kita di bangku SD, kita sudah dikenalkan tentang bilangan prima. Bilangan Prima adalah bilangan asli lebih dari 1 yang mempunyai faktor positif 1 dan bilangan itu sendiri.
2 adalah bilangan prima, karena faktor positif dari 2 adalah 1 dan 2
3 adalah bilangan prima, karena faktor positif dari 3 adalah 1 dan 3
4 adalah bukan bilangan prima, karena faktor positif dari 4 adalah 1, 2, dan 4 (ada sebanyak 3 faktor positif)
5 adalah bilangan prima, karena faktor positif dari 5 adalah 1 dan 5
6 adalah bukan bilangan prima, karena faktor positif dari 6 adalah 1, 2, 3, dan 6 (ada sebanyak 4 faktor positif)

…

Di bawah ini adalah semua bilangan prima dari 1 sampai 100.

$2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97$

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Ada sebanyak 25 bilangan prima yang kurang dari 100.

Baca juga Bilangan prima ke-1 sampai bilangan prima ke-500. Lengkap dengan nomor urutnya, jadi pembaca bisa tahu, bilangan prima ke-1 adalah 2, dan bilangan prima ke-5 adalah 11, berapakah bilangan prima ke-100. Berapa bilangan prima ke 500?

Bilangan prima tersebut hanya satu yang merupakan bilangan genap, yaitu $2$ . Karena bilangan genap selanjutnya merupakan bilangan kelipatan $2$ , sehingga bilangan genap selain $2$ adalah bilangan komposit.

Bilangan prima kurang dari 100 yang berakhiran 1 yaitu : 11, 31, 41, 61, dan 71
Bilangan prima kurang dari 100 yang berakhiran 3 yaitu : 3, 13, 23, 53, 73, dan 83
Bilangan prima kurang dari 100 yang berakhiran 7 yaitu : 7, 17, 37, 47, 67, dan 97
Bilangan prima kurang dari 100 yang berakhiran 9 yaitu : 19, 29, 59, 79, dan 89

Untuk pembaca yang ingin mempunyai aplikasi pencari bilangan prima, bisa langsung download saja di link berikut :
Download Aplikasi Bilangan Prima Versi Asimtot
Sekilas screenshot aplikasinya :

Semoga postingan ini membantu pembaca yang mencari bilangan prima kurang dari 100. (Kebanyakan memang tugas untuk anak SD untuk mencari bilangan prima yang kurang dari 100)

Baca juga tentang Bilangan Prima menarik yang lainnya, antara lain :

Bilangan prima dengan bentuk n^n + n | Hanya ada 1 bilangan prima yang berbentuk seperti itu
Versi baru software Bilangan Prima Asimtot (versi 2.0) | Aplikasi untuk mencari bilangan prima, aplikasi ini untuk PC, silahkan didownload gratis
7 bilangan prima unik versi asimtot | Mendengar bilangan prima unik mungkin jadi penasaran, sekedar pengetahuan saja supaya tidak jenuh. Mau tahu, masuk aja
Kuadrat bilangan prima jika dibagi 24 akan bersisa 1 | Silahkan langsung cek menuju TKP
Bilangan prima lebih besar 4 bisa ditulis menjadi 6n + 1 atau 6n – 1 | Ini adalah sifat dasar dari bilangan prima, cek
Bilangan Prima 1 sampai 100 | Bagi sobat yang ingin mencari semua bilangan prima dari 1 sampai 100
Multiplier pada bilangan prima | Multiplier pasti ada hubungannya dengan ciri bilangan yang habis dibagi. Bagaimana ciri bilangan habis dibagi 7, bagaimana ciri bilangan habis dibagi 19, ciri bilangan yang habis dibagi bilangan prima, ada kaitannya erat dengan yang namanya multiplier, cek
Bilangan prima unik dari kombinasi angka 1 dan 3 | Penasaran bagaimana bilangan prima dari kombinasi angka 1 dan 3
14 bilangan prima 2-digit yang jika disisipkan angka 0, membentuk bilangan prima 3-digit | Bilangan disisipi angka nol jadi bilangan prima, berapa saja yaaa

Adakah bilangan prima yang berbentuk $n^n + n$

Sekedar muncul di benak, suatu pertanyaan sederhana. Iseng aja saya tuliskan di blog ini. Habisnya, saya sudah lama tidak posting di blog kesayangan satu ini.

Bentuk $n^n + n$
Jika n genap, maka n^n genap mengapa??, tentu saja n^n + n juga genap
Jika n ganjil, maka n^n ganjil, mengapa?? tentu saja n^n + n hasilnya genap

Bilangan prima genap hanya ada satu, yaitu 2
Tentu saja untuk n=1, maka n^n + n = 2

Jadi hanya ada 1 bilangan prima yang berbentuk n^n + n, yaitu ketika n=1, n^n + n = 2

Keluarga Bilangan Prima

Bilangan prima memang tidak bisa ditebak. Ada yang ini dan ada yang seperti itu. Kalau tulisan sebelumnya membahas tentang bilangan prima yang membentuk palindrome, maka kali ini beda lagi. Kali ini yang akan dibahas adalah mengenai keluarga bilangan prima dan juga kawan-kawannya.

Bilangan dengan bentuk “m3”, dengan m adalah angka. Ini membentuk suatu keluarga yang sakinah, mawaddah dan warahmah. Hehe. Bilangan prima yang seperti itu ada sebanyak 6 bilangan, yaitu

$13, \quad 23, \quad 43, \quad 53, \quad 73, \quad 83$

Ada lagi keluarga bilangan prima yang banyaknya adalah 6 bilangan. Bilangan yang dibentuk adalah “56kk3”, dengan k adalah angka. Ada 6 bilangan dengan bentuk seperti itu yang merupakan bilangan prima, yaitu

$56003, \quad 56113, \quad 56333, \quad 56663, \quad 56773, \quad 56883$

Uniknya bilangan prima ya seperti ini. Ada lagi yang menarik, tentang kawan bilangan prima. Dua bilangan prima yang sangat erat hubungan pertemanannya. Sehingga jika mereka bergandengan akan membentuk bilangan prima juga. Digandeng di sebelah kanan membentuk bilangan prima dan digandeng di sebelah kiri juga membentuk suatu bilangan prima.
Dua bilangan itu adalah 7 dan 109.
Ketika mereka bergandengan, 7109, membentuk bilangan prima. Jika mereka bergandengan dengan posisi yang berbeda dari sebelumnya, 1097, juga merupakan bilangan prima.

Ini juga di miliki oleh bilangan prima 7 dan 3. Ketika mereka bergandengan juga membentuk bilangan prima. 73 merupakan bilangan prima dan 37 juga merupakan bilangan prima.

Dimiliki juga oleh 11 dan 3. 113 merupakan bilangan prima dan 311 juga merupakan bilangan prima.

Selain bilangan prima kawan, juga ada yang kami namakan bilangan prima looping. Bilangan prima memutar. Bilangan itu adalah 197, 971 dan 719. Ketiganya merupakan bilangan prima. Ini bisa dikatakan looping karena $1-9-7$ jika diputar terus juga akan menghasilkan bilangan prima. Sehingga kami menyebutnya looping.
Bilangan prima memang sangatlah menarik untuk dikaji. Meskipun rumus umum bilangan prima itu sendiri belum ada.

Ada juga yang menarik pada bilangan prima, yaitu mengenai Truncatable prime. Bilangan prima truncatable. Bilangan prima yang jika dihapus angka-angkanya dari kanan atau dari kiri (satu per satu) akan selalu membentuk bilangan prima.
Contohnya 73. Jika dihapus dari kanan akan didapatkan angka 7 yang merupakan bilangan prima. Jika dihapus angkanya dari kiri, maka akan didapatkan angka 3 yang juga merupakan bilangan prima.

Truncatable prime ini adalah cukup menarik perhatian untuk dicari. Bilangan truncatable prime ini misalnya yaitu 3797. Ketika kita hapus angkanya dari kanan (satu per satu), maka akan diperoleh sebagai berikut :

$3797 \quad \to \quad 379 \quad \to \quad 37 \quad \to \quad 3$

Semuanya merupakan bilangan prima. Jika angka-angkanya kita hapus dari kiri (satu per satu), maka akan diperoleh bentuk berikut :

$3797 \quad \to \quad 797 \quad \to \quad 97 \quad \to \quad 7$

Kesemuanya juga merupakan bilangan prima.

Mempunyai Faktor Bilangan Prima saja

Suatu bilangan yang mempunyai faktor positif yaitu bilangan prima saja (bilangan 1 dan dirinya sendiri memang sebagai faktor, tetapi di sini kita tidak menghitungnya). Misalnya 14, mempunyai faktor-faktor positif yaitu 1, 2, 7 dan 14. (untuk selanjutnya [pada tulisan ini saja] kita tidak menuliskan 1 dan dirinya sendiri sebagai faktor). Jadi faktor positifnya (tanpa dirinya sendiri dan satu) adalah 2 dan 7, yang keduanya merupakan bilangan prima.
Inilah yang selanjutnya kita sebut sebagai bilangan yang mempunyai faktor positif berupa bilangan prima saja.

Bilangan yang mempunyai faktor prima saja ini bisa juga didapatkan dari mengalikan bilangan prima yang berbeda. Misalnya kita mengalikan sebarang bilangan prima berbeda seperti berikut :

$2 \times 5=10$

10 adalah bilangan yang mempunyai faktor prima saja. Mudah dicari untuk bilangan-bilangan yang seperti ini. Hanya dengan mengalikan dua bilangan prima yang berbeda, kita pasti mendapatkan bilangan yang hanya mempunyai faktor prima saja. Mudah bukan.

Pencarian kami tidak berhenti begitu saja. Kami menemukan banyak yang unik mengenai bilangan yang seperti ini. Bilangan yang mempunyai faktor positif berupa bilangan prima saja. Misalnya kapan pertama kalinya bilangan yang seperti itu didapatkan berurutan? Apa ada bilangan seperti itu yang membentuk suatu palindrom? Dan mungkin pertanyaan-pertanyaan dari para pembaca.

Bilangan yang hanya mempunyai faktor prima saja yang merupakan bilangan palindrom.

Kita sudah mengetahui cara untuk mendapatkan suatu bilangan yang hanya mempunyai faktor prima saja. beberapa berikut ini adalah bilangan tersebut yang membentuk palindrom.

$22,33,55,77$

Bilangan-bilangan tersebut sudah sangat jelas akan membentuk palindrom.
Berikutnya adalah sebagai berikut :

$111=3 \times 37$

$141=3 \times 47$

$161=7 \times 23$

$737=67 \times 11$

$989=23 \times 43$

$979=11 \times 89$

Dua bilangan berurutan yang keduanya merupakan bilangan yang hanya mempunyai faktor positif bilangan prima saja adalah sebagai berikut :

$14=7 \times 2$ dan $15=5 \times 3$

14 dan 15 ini adalah bilangan pertama yang membentuk seperti itu. Bilangan-bilangan selanjutnya sangat banyak sekali. Berikut ini adalah bilangan-bilangannya

$33=11 \times 3$ dan $34=17 \times 2$
$38=19 \times 2$ dan $39=13 \times 3$
$122=61 \times 2$ dan $123=41 \times 3$

Ada juga yang unik yang merupakan bilangan yang mempunyai faktor prima saja. yaitu bilangan berbalik ini, 26 dan 62 yang keduanya merupakan bilangan yang hanya mempunyai faktor bilangan prima saja.

$26=13 \times 2$

$62=31 \times 2$

Selain itu bilangan berbalik yang juga merupakan bilangan yang mempunyai faktor prima saja adalah bilangan berbalik 319 dan 913. Dan ternyata kombinasi dari 3, 1 dan 9 yang membentuk bilangan 391 juga merupakan bilangan yang hanya mempunyai faktor berupa bilangan prima saja. 1309 dan 1139 juga merupakan bilangan yang hanya mempunyai faktor berupa bilangan prima.

$319=11 \times 29$
$913=11 \times 83$
$391=17 \times 23$
$1309=11 \times 119$
$1139=17 \times 67$

143 dan 341 juga merupakan bilangan berbalik yang keduanya merupakan bilangan yang hanya mempunyai faktor positif berupa bilangan prima saja. $11 \times 13=143$ dan $31 \times 11=341$ .

Menuju ke yang lainnya. Bilangan yang hanya mempunyai faktor bilangan prima saja ini juga mempunyai keunikan yang lainnya.

$119$

Jika kita rotasikan 180 derajat, maka akan menjadi

$611$

Keduanya merupakan bilangan yang hanya mempunyai faktor berupa bilangan prima saja. $119=17 \times 7$ dan $611=13 \times 47$ . Perhatikan angka-angka yang ada pada bilangan prima yang menjadi faktor tersebut. 17 dan 7. Jika angka-angkanya kita jumlahkan maka diperoleh $1+7+7=15$ . 13 dan 47. Jika angka-angkanya kita jumlahkan maka kita mendapatkan $1+3+4+7=15$ . Ini setara dengan $9+6=15$ . Rotasi kita tadi menyebabkan 6 menjadi 9. Angka 1 tetap menjadi angka 1, jadi kita tidak menghitungnya.

15 sendiri adalah bilangan yang hanya mempunyai faktor berupa bilangan prima saja. 15 yang berasal dari perkalian bilangan prima 5 dan 3.

7 bilangan prima unik versi asimtot

Bilangan prima satu ini adalah satu-satunya bilangan prima yang genap.Tidak ada bilangan prima lagi selain 2 yang merupakan bilangan genap.
Bilangan genap yang lain pasti merupakan bilangan kelipatan 2, sehingga bilangan-bilangan genap kecuali 2 pasti bukan merupkan bilangan prima.
Selain itu, bilangan 2 adalah bilangan prima yang pertama. Bilangan prima pertama dan satu-satunya bilangan prima yang genap. Unik kan!
Bilangan prima ditambah 1 sama dengan bilangan komposit (kecuali pada bilangan prima 2). Karena $2+1=3$ yang juga merupakan bilangan prima. Lagi-lagi melibatkan bilangan prima 2. Hehehe.

Bilangan prima pertama yang membentuk palindrom.
Bilangan prima pertama dengan angka berulang.
Satu-satunya bilangan prima 2-angka yang membentuk palindrom.
Satu-satunya bilangan prima n-angka (dengan n bilangan genap) yang membentuk palindrom. Karena, bilangan palindrome n-angka (dengan n genap) adalah bilangan kelipatan 11.
Selain itu, bilangan prima 11 adalah bilangan prima 2-angka yang pertama.
Bilangan prima 11 juga banyak keunikannya. Perkalian dengan bilangan 11, lalu bilangan palindron yang berdigit sebanyak bilangan genap merupakan kelipatan 11. Ada lagi bilangan prima yang mempunyai angka-angka 1, yaitu 1111111111111111111 (sebanyak 19 angka 1). Unik bukan.

13 dan 31

Bilangan prima pertama yang jika angka-angkanya dibaca dari belakang juga membentuk bilangan prima. Bilangan prima yang kedua yaitu 17, karena 71 juga merupakan bilangan prima. Sebenarnya banyak bilangan yang dibaca dan dibaca dari belakang membentuk bilangan prima. Tetapi karena 13 dan 31 merupakan bilangan yang pertama, jadi ya kita memilihnya sebagai bilangan prima unik.

2011

Tahun baru ini adalah menyambut tahun 2011. Dan 2011 adalah bilangan prima. Kita akan memasuki tahun prima. Tidak ada hal khusus memang di tahun yang prima. Hanya keunikan tahunnya saja yang merupakan bilangan prima.
Di tahun prima ini memang tidak ada hal yang unik. Kita bikin unik sendiri saja. Apakah hari ulang tahunmu nanti juga merupakan bilangan prima, misalnya 7052011, yaitu tanggal 7 bulan 5 tahun 2011 merupakan bilangan prima. Apakah hari ulang tahunmu di tahun 2011 merupakan bilangan prima?

11112011

Bilangan prima unik. 11112011.Bukan palindrom memang. Tetapi, ini unik karena antara tanggal, bulan dan tahunnya mempunyai angka-angka 1. Bila dituliskan dalam penulisan singkat, 11-11-11. Padahal jika dituliskan secara panjang, ini adalah suatu bilangan prima. Kami mempunyai sesuatu yang unik di sini, pada tanggal 11 bulan 11 tahun 2011. Tunggu saja.

23456789

Bilangan prima unik yang terdiri dari angka berurutan. 23456789. Siapa sangka kalau bilangan tersebut adalah bilangan prima. Bilangan prima ini kami pilih sebagai bilangan prima unik karena angka-angkanya berurutan dari 2 sampai 9.
Unik bukan.

345676543

Bilangan prima unik yang angka-angkanya naik kemudian turun ke angka awal. Bilangan ini membentuk palindrom. Perhatikan angka-angka dari bilangan prima yang satu ini. Dari angka 3 kemudian naik ke 4, 5 dan sampai di 7 turun lagi ke 3.

Aplikasi Bilangan Prima

Asimtot telah sedikit memperbaiki software bilangan primanya.
Bagi yang belum tahu software bilangan prima versi lama, silahkan bisa dicoba. Portable.
Download di sini
Software Bilangan Prima versi 1.0
Software Bilangan Prima versi 1.3

Software terbaru adalah Software Bilangan Prima versi 2.0, silahkan di download di sini : Software Bilangan Prima versi 2.0
Fitur versi 2.0 ini adalah
– Proses perhitungan semakin cepat (berbeda jauh kecepatannya dibandingkan versi 1.3)
– Ada fitur lain-lain tentang prima
– Mencari bilangan prima yang berakhiran 1. Atau 2, 3, dst
– Menampilkan konjecture Goldbach 1 (semua kemungkinan akan dituliskan)
– Desain yang cukup berbeda dengan versi sebelumnya
Screenshotnya :

Untuk Konjecturenya

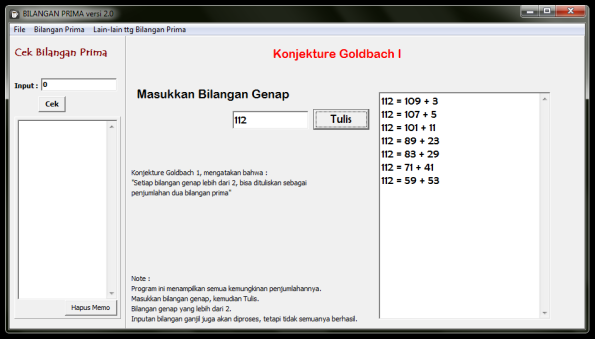
Silahkan dicoba sendiri. Ukuran kecil. Tidak lebih dari 1 Mb.
Ditunggu saran dan kritikannya

Semua Tentang Bilangan Prima

Bilangan Prima

Adakah bilangan prima yang berbentuk $n^n + n$

Keluarga Bilangan Prima

Mempunyai Faktor Bilangan Prima saja

7 bilangan prima unik versi asimtot

Aplikasi Bilangan Prima

0 Response to "Semua Tentang Bilangan Prima"

Posting Komentar

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel