Aturan rantai pada turunan
Bagaimana mencari turunan? Dengan menggunakan definisinya, atau
dengan menggunakan sifat-sifatnya? Kapan selesainya jika menyelesaikan
turunan dengan menggunakan definisinya. Hehehe..
Tidak sampai di situ, kami ingatkan saja mengenai definisinya :

Tentunya kita masih ingat definisi tersebut. Harus ingat!
Kembali ke judulnya, yaitu aturan rantai pada turunan. Bagaimana aturan rantai pada turunan, kita simak saja di bawah ini :
Bagaimana menyelesaikan ini, tentukan turunan dari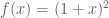 !
!
Tentunya kita bisa menyelesaikannya dengan aturan pangkat pada turunan. Kita jacbarkan terlebih dahulu dengan menggunakan binomial. Menjadi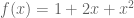 . Kemudian kita cari turunannya, yaitu
. Kemudian kita cari turunannya, yaitu 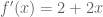
Ini sangatlah mudah, bagaimanakan menyelesaikan ini, tentukan turunan dari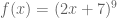 . Apakah kita akan menjabarkannya dengan menggunakan binomial dan memakan waktu yang sangat lama? Tentunya tidak.
. Apakah kita akan menjabarkannya dengan menggunakan binomial dan memakan waktu yang sangat lama? Tentunya tidak.
Kita bisa menyelesaikan bentuk ini dengan aturan rantai. Bagaimana aturan rantai itu?
Seperti berikut :

Untuk lebih memudahkan pemahaman, kita ke contoh soal saja.
Kembali ke soal sebelumnya, bagaimana menyelesaikan ini, tentukan turunan dari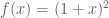
akan kita gunakan aturan rantai pada turunan yang ada di atas.
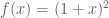
Misalkan saja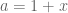 . Turunan dari a terhadap x adalah 1. Dan sekarang bentuk awal bisa kita tulis
. Turunan dari a terhadap x adalah 1. Dan sekarang bentuk awal bisa kita tulis

Tentu, dengan menggunakan aturan pangkat, kita peroleh :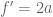
Kita kembalikan pemisalan kita tadi, yaitu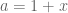
Sehingga, diperoleh,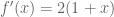
Hasilnya sama kan!
Untuk lebih mudahnya, Turunkan saja pangkatnya, kalikan dengan turunan yang ada di dalamnya.
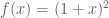

Bagaimana dengan soal kedua :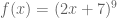
Maka, dengan mudah, kita bisa menentukannya, yaitu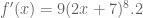
Maka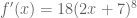
Latihan :
Tentukan bentuk turunannya!
a).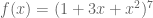
b).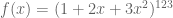
c).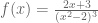
Tidak sampai di situ, kami ingatkan saja mengenai definisinya :
Turunan sebuah fungsi f adalah f’ (dibaca : “f aksen”) yang nilainya pada sebarang bilangan c adalah
asalkan limit ini ada dan bukan 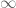 atau
atau 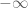
Tentunya kita masih ingat definisi tersebut. Harus ingat!
Kembali ke judulnya, yaitu aturan rantai pada turunan. Bagaimana aturan rantai pada turunan, kita simak saja di bawah ini :
Bagaimana menyelesaikan ini, tentukan turunan dari
Tentunya kita bisa menyelesaikannya dengan aturan pangkat pada turunan. Kita jacbarkan terlebih dahulu dengan menggunakan binomial. Menjadi
Ini sangatlah mudah, bagaimanakan menyelesaikan ini, tentukan turunan dari
Kita bisa menyelesaikan bentuk ini dengan aturan rantai. Bagaimana aturan rantai itu?
Seperti berikut :
Andaikan  dan
dan 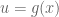 . Jika g terdiferensiasikan di x dan f terdiferensiasikan di u. Maka fungsi komposit
. Jika g terdiferensiasikan di x dan f terdiferensiasikan di u. Maka fungsi komposit  yang didefinisikan oleh
yang didefinisikan oleh  terdiferensiasikan di x dan
terdiferensiasikan di x dan
Untuk lebih memudahkan pemahaman, kita ke contoh soal saja.
Kembali ke soal sebelumnya, bagaimana menyelesaikan ini, tentukan turunan dari
akan kita gunakan aturan rantai pada turunan yang ada di atas.
Misalkan saja
Tentu, dengan menggunakan aturan pangkat, kita peroleh :
Kita kembalikan pemisalan kita tadi, yaitu
Sehingga, diperoleh,
Hasilnya sama kan!
Untuk lebih mudahnya, Turunkan saja pangkatnya, kalikan dengan turunan yang ada di dalamnya.
Bagaimana dengan soal kedua :
Maka, dengan mudah, kita bisa menentukannya, yaitu
Maka
Latihan :
Tentukan bentuk turunannya!
a).
b).
c).
0 Response to "Aturan rantai pada turunan"
Posting Komentar
Harap komentar yang bijak!!!