Integral substitusi
Setelah kemarin membahas mengenai integral dan kemarin hanya
diberikan sifat pangkat pada integral dan linear saja. kali ini akan
diberikan integral yang terhitung masih sederhana, tetapi sudah berada
di tingkat di atas dari aturan pangkat, yaitu integral substitusi.
Sebelum masuk ke integral substitusi, kita perhatikan terlebih dahulu hal berikut :
Bagaimana mengerjakan bentuk :
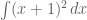
Tentu kita bisa menjabarkannya dan selanjutnya menggunakan aturan pangkat. Untuk menjabarkan bentuk pangkat tersebut, kita harus ingat dengan binomial newton.
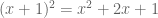
Sehingga, bentuk integral pada soal pun bisa dituliskan menjadi
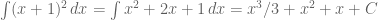
Lalu, bagaimana kalau kita bertemu dengan soal ini :
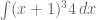
Apakah kita harus menjabarkannya? Tentu akan memakan waktu yang sangat lama.
Kita akan mempelajari teknik integral yang sering disebut sebagai integral substitusi. Untuk itu, kita kerjakan terlebih dahulu untuk soal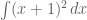 dengan menggunakan aturan substitusi.
dengan menggunakan aturan substitusi.
Di dalam aturan substitusi kita akan menggunakan pemisalan. Pada soal tersebut, langkah-langkahnya sebagai berikut : misalkan,
 , maka
, maka 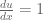 , maka
, maka 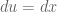
Sehingga, bentuk soal bisa dituliskan sebagai berikut :
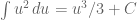
Karena yang diinginkan adalah variabel x, maka masukkan kembali bentuk yang tadi. Sehingga diperoleh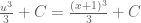
Dengan cara seperti ini, maka bentuk soal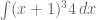 akan mudah diselesaikan. Berikut langkah penyelesaiannya, yaitu dengan memisalkan
akan mudah diselesaikan. Berikut langkah penyelesaiannya, yaitu dengan memisalkan 
Contoh soal
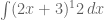
Penyelesaian :
Misalkan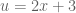 , maka
, maka  , maka
, maka 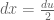
Kita kembali ke soal, sehingga soal menjadi :

Silahkan dilanjutkan. ..
Soal yang bukan menggunakan substitusi misalnya
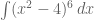
Soal seperti ini tidak bisa menggunakan aturan substitusi seperti di atas. Silahkan dicoba dengan menggunakan pemisalan seperti contoh-contoh di atas. Nanti, akan ditemukan sesuatu yang mengakibatkan langkah itu tidak bisa dilanjutkan.
Berbeda dengan soal berikut, yang bisa menggunakan aturan substitusi
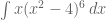
Soal ini bisa menggunakan substitusi, yaitu dengn memisalkan
 , maka
, maka 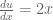 , sehingga
, sehingga 
Soal pun bisa dituliskan dalam bentuk
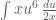
Akhirnya x nya bisa dicoret.. . sehingga menjadi bentuk berikut ini :
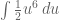
Silahkan dilanjutkan.. .
Latihan Soal


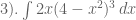

Sebelum masuk ke integral substitusi, kita perhatikan terlebih dahulu hal berikut :
Bagaimana mengerjakan bentuk :
Tentu kita bisa menjabarkannya dan selanjutnya menggunakan aturan pangkat. Untuk menjabarkan bentuk pangkat tersebut, kita harus ingat dengan binomial newton.
Sehingga, bentuk integral pada soal pun bisa dituliskan menjadi
Lalu, bagaimana kalau kita bertemu dengan soal ini :
Apakah kita harus menjabarkannya? Tentu akan memakan waktu yang sangat lama.
Kita akan mempelajari teknik integral yang sering disebut sebagai integral substitusi. Untuk itu, kita kerjakan terlebih dahulu untuk soal
Di dalam aturan substitusi kita akan menggunakan pemisalan. Pada soal tersebut, langkah-langkahnya sebagai berikut : misalkan,
Sehingga, bentuk soal bisa dituliskan sebagai berikut :
Karena yang diinginkan adalah variabel x, maka masukkan kembali bentuk yang tadi. Sehingga diperoleh
Dengan cara seperti ini, maka bentuk soal
Contoh soal
Penyelesaian :
Misalkan
Kita kembali ke soal, sehingga soal menjadi :
Silahkan dilanjutkan. ..
Soal yang bukan menggunakan substitusi misalnya
Soal seperti ini tidak bisa menggunakan aturan substitusi seperti di atas. Silahkan dicoba dengan menggunakan pemisalan seperti contoh-contoh di atas. Nanti, akan ditemukan sesuatu yang mengakibatkan langkah itu tidak bisa dilanjutkan.
Berbeda dengan soal berikut, yang bisa menggunakan aturan substitusi
Soal ini bisa menggunakan substitusi, yaitu dengn memisalkan
Soal pun bisa dituliskan dalam bentuk
Akhirnya x nya bisa dicoret.. . sehingga menjadi bentuk berikut ini :
Silahkan dilanjutkan.. .
Latihan Soal
0 Response to "Integral substitusi"
Posting Komentar
Harap komentar yang bijak!!!