Integral (bagian 1)
Definisi : kita menyebut F suatu antiturunan f pada selang I jika 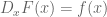 pada I – yakni, jika
pada I – yakni, jika 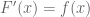 untuk semua x dalam I. (Jika x titik ujung dari I,
untuk semua x dalam I. (Jika x titik ujung dari I,  hanya perlu turunan sepihak)
hanya perlu turunan sepihak)
Kita sudah mengenal turunan, dan sekarang kita akan mengenal yang namanya antiturunan (Integral). Turunan, antiturunan.. . hehe.
Notasi untuk integral ini adalah awalnya yaitu , tetapi kemudian Leibniz mengenalkan lambang
, tetapi kemudian Leibniz mengenalkan lambang 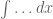 . Dan sekarang kita menggunakan notasi leibniz untuk lambang integral.
. Dan sekarang kita menggunakan notasi leibniz untuk lambang integral.
Cukup bayangkan bentuk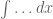 sebagai sesuatu yang menunjukkan suatu antiturunan terhadap x, Sama seperti
sebagai sesuatu yang menunjukkan suatu antiturunan terhadap x, Sama seperti 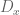 yang menunjukkan suatu turunan terhadap x
yang menunjukkan suatu turunan terhadap x
Perhatikan bahwa
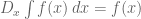 dan
dan 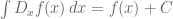 Aturan pangkat
Aturan pangkat
Aturan yang paling sederhana pada suatu integral. Aturan pangkat sebagai berikut :
Jika r adalah suatu bilangan real dan r tidak sama dengan -1, maka
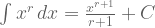
Aturan pangkat adalah aturan yang sangat sederhana dan diharapkan pembaca sudah menguasai ini diluar kepala.
Selain aturan pangkat, ada beberapa sifat integral yang perlu diketahui. Yaitu sifat kelinearan integral. Jika f
Dan g mempunyai antiturunan, dan andaikan k adalah konstanta, maka
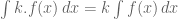

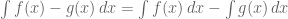
3 Sifat ini penting untuk diingat. Karena beberapa bentuk integral menggunakan kunci sifat-sifat ini. Ingat. bentuk tersebut tidak ada yang perkalian fungsi dengan fungsi lain.
TIDAK BERLAKU
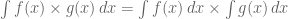
Tidak berlaku pada perkalian dan pembagian.. . Ingat!
Latihan Soal :



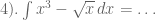
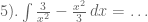
Kita sudah mengenal turunan, dan sekarang kita akan mengenal yang namanya antiturunan (Integral). Turunan, antiturunan.. . hehe.
Notasi untuk integral ini adalah awalnya yaitu
Cukup bayangkan bentuk
Perhatikan bahwa
Aturan yang paling sederhana pada suatu integral. Aturan pangkat sebagai berikut :
Jika r adalah suatu bilangan real dan r tidak sama dengan -1, maka
Aturan pangkat adalah aturan yang sangat sederhana dan diharapkan pembaca sudah menguasai ini diluar kepala.
Selain aturan pangkat, ada beberapa sifat integral yang perlu diketahui. Yaitu sifat kelinearan integral. Jika f
Dan g mempunyai antiturunan, dan andaikan k adalah konstanta, maka
3 Sifat ini penting untuk diingat. Karena beberapa bentuk integral menggunakan kunci sifat-sifat ini. Ingat. bentuk tersebut tidak ada yang perkalian fungsi dengan fungsi lain.
TIDAK BERLAKU
Tidak berlaku pada perkalian dan pembagian.. . Ingat!
Latihan Soal :
0 Response to "Integral (bagian 1)"
Posting Komentar
Harap komentar yang bijak!!!