Mengutak-atik barisan fibonacci menjadi konvergen
Sudah kita kenal bagaimana barisan fibonacci itu. Beberapa suku awalnya adalah :
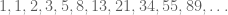
Barisan fibonacci ini menggunakan rumus rekursif yaitu untuk
untuk 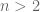 dengan
dengan 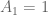 dan
dan 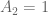 . Tentu di sini n adalah himpunan bilangan asli.
. Tentu di sini n adalah himpunan bilangan asli.
Tentu, barisan fibonacci ini merupakan barisan yang divergen. Karena bilangan-bilangannya semakin membesar mendekati tak hingga. Deret fibonacci juga divergen karena jumlahnya mendekati tak hingga.
Berikut adalah deret fibonacci yang dimodif sehingga jumlah deret tak hingganya adalah mempunyai nilai (terhingga).
Kita mengenal deret berikut ini :
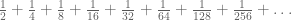
Kina mengenal barisan tersebut sebagai barisan yang konvergen. Bagaimana menunjukkannya? Seperti berikut :
Misalkan :
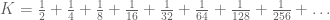
Jikan kedua ruas kita kalikan dengan 2, kita peroleh :

Kedua ruas kita kurangi dengan 1. Kita peroleh :
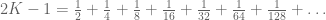
Ini sama dengan pemisalan kita tadi, sehingga kita peroleh :

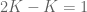
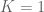
Jadi, kita peroleh bahwa :
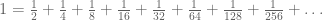
Ini juga bisa dicari dengan menggunakan rumus deret geometri tak hingga dengan suku pertama yaitu setengah dan rasionya adalah setengah.
Jika masing masing suku penjumlahannya diberikan bilangan fibonacci secara berurutan, bagaimanakah dengan jumlahnya?
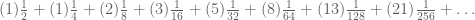
Bagaimana dengan jumlahnya?
Perhatikan tabel berikut ini :
Ternyata nilainya mendekati 2.
Dan memang barisan tersebut akan konvergen ke 2.
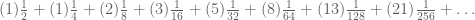
Akan konvergen ke 2.
Barisan fibonacci ini menggunakan rumus rekursif yaitu
Tentu, barisan fibonacci ini merupakan barisan yang divergen. Karena bilangan-bilangannya semakin membesar mendekati tak hingga. Deret fibonacci juga divergen karena jumlahnya mendekati tak hingga.
Berikut adalah deret fibonacci yang dimodif sehingga jumlah deret tak hingganya adalah mempunyai nilai (terhingga).
Kita mengenal deret berikut ini :
Kina mengenal barisan tersebut sebagai barisan yang konvergen. Bagaimana menunjukkannya? Seperti berikut :
Misalkan :
Jikan kedua ruas kita kalikan dengan 2, kita peroleh :
Kedua ruas kita kurangi dengan 1. Kita peroleh :
Ini sama dengan pemisalan kita tadi, sehingga kita peroleh :
Jadi, kita peroleh bahwa :
Ini juga bisa dicari dengan menggunakan rumus deret geometri tak hingga dengan suku pertama yaitu setengah dan rasionya adalah setengah.
Jika masing masing suku penjumlahannya diberikan bilangan fibonacci secara berurutan, bagaimanakah dengan jumlahnya?
Bagaimana dengan jumlahnya?
Perhatikan tabel berikut ini :
|
n
|
Setengah pangkat n
|
fibonacci
|
Nilai suku ke-n
|
Jumlah sampai suku ke-n
|
|
|
1
|
0,5
|
1
|
0,5
|
0,5
|
|
|
2
|
0,25
|
1
|
0,25
|
0,75
|
|
|
3
|
0,125
|
2
|
0,25
|
1
|
|
|
4
|
0,0625
|
3
|
0,1875
|
1,1875
|
|
|
5
|
0,03125
|
5
|
0,15625
|
1,34375
|
|
|
6
|
0,015625
|
8
|
0,125
|
1,46875
|
|
|
7
|
0,0078125
|
13
|
0,1015625
|
1,5703125
|
|
|
8
|
0,00390625
|
21
|
0,08203125
|
1,65234375
|
|
|
9
|
0,001953125
|
34
|
0,06640625
|
1,71875
|
|
|
10
|
0,000976563
|
55
|
0,053710938
|
1,772460938
|
|
|
11
|
0,000488281
|
89
|
0,043457031
|
1,815917969
|
|
|
12
|
0,000244141
|
144
|
0,03515625
|
1,851074219
|
|
|
13
|
0,00012207
|
233
|
0,028442383
|
1,879516602
|
|
|
14
|
6,10352E-05
|
377
|
0,023010254
|
1,902526855
|
|
|
15
|
3,05176E-05
|
610
|
0,018615723
|
1,921142578
|
|
|
16
|
1,52588E-05
|
987
|
0,015060425
|
1,936203003
|
|
|
17
|
7,62939E-06
|
1597
|
0,012184143
|
1,948387146
|
|
|
18
|
3,8147E-06
|
2584
|
0,009857178
|
1,958244324
|
|
|
19
|
1,90735E-06
|
4181
|
0,007974625
|
1,966218948
|
|
|
20
|
9,53674E-07
|
6765
|
0,006451607
|
1,972670555
|
|
|
21
|
4,76837E-07
|
10946
|
0,00521946
|
1,977890015
|
|
|
22
|
2,38419E-07
|
17711
|
0,004222631
|
1,982112646
|
|
|
23
|
1,19209E-07
|
28657
|
0,003416181
|
1,985528827
|
|
|
24
|
5,96046E-08
|
46368
|
0,002763748
|
1,988292575
|
|
|
25
|
2,98023E-08
|
75025
|
0,002235919
|
1,990528494
|
|
|
26
|
1,49012E-08
|
121393
|
0,001808897
|
1,992337391
|
|
|
27
|
7,45058E-09
|
196418
|
0,001463428
|
1,993800819
|
|
|
28
|
3,72529E-09
|
317811
|
0,001183938
|
1,994984757
|
|
|
29
|
1,86265E-09
|
514229
|
0,000957826
|
1,995942583
|
|
|
30
|
9,31323E-10
|
832040
|
0,000774898
|
1,996717481
|
|
|
31
|
4,65661E-10
|
1346269
|
0,000626905
|
1,997344386
|
|
|
32
|
2,32831E-10
|
2178309
|
0,000507177
|
1,997851563
|
|
|
33
|
1,16415E-10
|
3524578
|
0,000410315
|
1,998261878
|
|
|
34
|
5,82077E-11
|
5702887
|
0,000331952
|
1,99859383
|
|
|
35
|
2,91038E-11
|
9227465
|
0,000268555
|
1,998862385
|
|
|
36
|
1,45519E-11
|
1,5E+07
|
0,000217265
|
1,99907965
|
|
|
37
|
7,27596E-12
|
2,4E+07
|
0,000175771
|
1,999255421
|
|
|
38
|
3,63798E-12
|
3,9E+07
|
0,000142202
|
1,999397623
|
|
|
39
|
1,81899E-12
|
6,3E+07
|
0,000115044
|
1,999512667
|
|
|
40
|
9,09495E-13
|
1E+08
|
9,30724E-05
|
1,999605739
|
|
|
41
|
4,54747E-13
|
1,7E+08
|
7,52971E-05
|
1,999681036
|
|
|
42
|
2,27374E-13
|
2,7E+08
|
6,09167E-05
|
1,999741953
|
|
|
43
|
1,13687E-13
|
4,3E+08
|
4,92826E-05
|
1,999791236
|
|
|
44
|
5,68434E-14
|
7E+08
|
3,98705E-05
|
1,999831106
|
|
|
45
|
2,84217E-14
|
1,1E+09
|
3,22559E-05
|
1,999863362
|
|
|
46
|
1,42109E-14
|
1,8E+09
|
2,60956E-05
|
1,999889457
|
|
|
47
|
7,10543E-15
|
3E+09
|
2,11118E-05
|
1,999910569
|
|
|
48
|
3,55271E-15
|
4,8E+09
|
1,70798E-05
|
1,999927649
|
|
|
49
|
1,77636E-15
|
7,8E+09
|
1,38178E-05
|
1,999941467
|
|
|
50
|
8,88178E-16
|
1,3E+10
|
1,11789E-05
|
1,999952646
|
Ternyata nilainya mendekati 2.
Dan memang barisan tersebut akan konvergen ke 2.
Akan konvergen ke 2.
0 Response to "Mengutak-atik barisan fibonacci menjadi konvergen"
Posting Komentar
Harap komentar yang bijak!!!