Mengubah bentuk desimal berulang ke dalam pecahan biasa (bagian 2)

Mengubah bentuk desimal berulang ke dalam pecahan biasa dengan menggunakan konsep deret geometri tak hingga. Banyak cara yang bisa dilakukan untuk mengubah bentuk desimal berulang menjadi bentuk pecahan. Misalnya saja untuk mengubah bentuk menjadi bentuk pecahan biasa. Cara biasa yang bisa kita lakukan adalah sebagai berikut :

Misalnya kemudian kita kalikan dengan 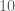. Dihasilkan

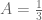
Dengan cara lain, yaitu dengan menggunakan konsep dari deret geometri tak hingga yang konvergen. Misalnya

pada contoh di atas. Kita akan merubah bentuk desimal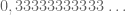 menjadi bentuk pecahan dengan menggunakan konsep deret geometri tak hingga yang konvergen.

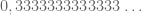bisa kita tuliskan sebagi penjumlahan dari




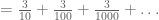
Bentuk tersebut adalah bentuk deret geometri dengan dan .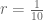

Kita bisa menentukan jumlahnya yaitu dengan menggunakan rumus , dengan adalah suku pertama dan adalah rasio. Dengan menggunakan rumus tersebut didapatkan :







Dengan cara yang berbeda, didapatkan hasil yang sama.

Share this post