Palindrom 4 angka selalu habis dibagi 11

Misalnya 1111. Merupakan palindrom dengan 4 digit. 1111 habis dibagi 11 yaitu hasilnya 101. Begitu juga dengan palindrom 4 digit yang lain. Misalnya 2332. Merupakan palindrom 4 digit. Dan 2332 habis dibagi 11. Hasilnya yaitu 212.
Mengapa bisa terjadi hal seperti itu?
Perhatikan ciri sebuah bilangan habis dibagi 11 berikut ini :
Sebuah bilangan habis dibagi 11 yaitu jika bilangan tersebut merupakan kelipatan 11. Ciri bilangan habis dibagi 11 yaitu jika jumlah digitnya dengan berganti tanda dari digit satuan hasilnya habis dibagi 11.

Misalnya

Apakah 1221 habis dibagi 11?
1 – 2 + 2 – 1 = 0. Karena 0 habis dibagi 11. Maka 1221 habis dibagi 11.
Untuk sebarang bilangan misalnya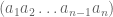 $(a_1 a_2 \dots a_{n-1} a_n)$ sebanyak n digit. Bentuk tersebut dapat kita tuliskan menjadi bentuk

$(a_1 a_2 \dots a_{n-1} a_n)=a_1 \times 10^{n-1} + a_2 \times 10^{n-2}+ \dots+ a_{n-1} \times 10 + a_n$

Sekarang kita perhatikan hal berikut ini :

1 = 0 + 1
10 = 11 – 1
100 = 99 + 1
1000 = 1001 – 1
10000 = 9999 + 1
…
dan seterusnya…

perhatikan bahwa 0, 11, 99, 1001, 9999, … merupakan kelipatan 11

$(a_1 a_2 \dots a_{n-1} a_n)=a_1 \times 10^{n-1} + a_2 \times 10^{n-2}+ \dots+ a_{n-2} \times 100 +a_{n-1} \times 10 + a_n$
$(a_1 a_2 \dots a_{n-1} a_n)=a_1 \times 10^{n-1} + a_2 \times 10^{n-2}+ \dots+ a_{n-2} \times (99+1) + a_{n-1} \times (11-1) + a_n$

Untuk memudahkan kita anggap banyaknya digitnya sebarang.

$( \dots a_{n-1} a_n)= \dots+ a_{n-2} \times (99+1) + a_{n-1} \times (11-1) + a_n$
$( \dots a_{n-1} a_n)= ( \dots + 99a_{n-2} + 11a_{n-1}) + ( \dots + a_{n-2} - a_{n-1} + a_n)$

Jika $( \dots a_{n-1} a_n)$ habis dibagi 11. Dan $( \dots + 99a_{n-2} + 11a_{n-1})$ habis dibagi 11. Maka haruslah $( \dots + a_{n-2} - a_{n-1} + a_n)$ habis dibagi 11. Jadi, ciri habis dibagi 11 adalah $( \dots + a_{n-2} - a_{n-1} + a_n)$ habis dibagi 11. Yaitu jumlah digitnya dengan berganti tanda dari digit satuan dimulai dari tanda positif hasilnya habis dibagi 11.

Dan sekarang kita perhatikan bahwa setiap bilangan palindrom 4 digit. Maka jika kita lakukan langkah ciri bilangan habis dibagi 11. Yaitu menjumlahkan digit-digitnya dari digit satuan dengan tanda positif terlebih dahulu. Maka nanti hasilnya pasti nol. Karena bilangan palindrom 4 digit berbentuk (aaaa) atau (abba). Untuk (aaaa) sudah pasti habis dibagi 11. Karena
a – a + a – a = 0
Untuk (abba), a – b + b – a = 0. Maka abba juga habis dibagi 11.

Dengan demikian terbukti bahwa bilangan berdigit 4 yang membentuk palindrom, habis dibagi 11.
Begitu juga untuk bilangan berdigit 2, 6, 8, 10, dst.. bisa dibuktikan sendiri.

Palindrom 4 angka selalu habis dibagi 11

0 Response to "Palindrom 4 angka selalu habis dibagi 11"

Posting Komentar

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel