Bentuk pangkat rasional
Jika kita ditanya, berapakah nilai dari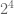 
. Dengan mudah kita bisa menjawab, bahwa sesuai definisi yang diberikan, maka
Kemudian kita ditanya lagi, berapakah nilai dari
. Bagaimana kita menjawabnya?
Di sinilah akan kita pelajari…
Sebelum masuk ke pangkat rasional. Tentunya kita harus tahu apa itu pangkat rasional terlebih dahulu. Pangkat rasional adalah bentuk pangkat pecahan. Rasio adalah perbandingan. Jadi,
pangkatnya itu berupa pecahan.
Sebelum kita masuk ke situ, mari kita lihat dulu beberapa sifat penting mengenai bentuk akar.
Jika a dan b sebarang bilangan real dan sebarang bilangan asli m dan n (dengan n tidak sama dengan 1), maka
1. Jika n genap, maka![\sqrt[n]{a^n}= \mid a \mid](https://s0.wp.com/latex.php?latex=%5Csqrt%5Bn%5D%7Ba%5En%7D%3D+%5Cmid+a+%5Cmid&bg=ffffff&fg=555555&s=0 "\sqrt[n]{a^n}= \mid a \mid")
2. jika n ganjil, maka![\sqrt[n]{a^n}=a](https://s0.wp.com/latex.php?latex=%5Csqrt%5Bn%5D%7Ba%5En%7D%3Da&bg=ffffff&fg=555555&s=0 "\sqrt[n]{a^n}=a")
3.![\sqrt[n]{a} \times \sqrt[n]{b}= \sqrt[n]{ab}](https://s0.wp.com/latex.php?latex=%5Csqrt%5Bn%5D%7Ba%7D+%5Ctimes+%5Csqrt%5Bn%5D%7Bb%7D%3D+%5Csqrt%5Bn%5D%7Bab%7D&bg=ffffff&fg=555555&s=0 "\sqrt[n]{a} \times \sqrt[n]{b}= \sqrt[n]{ab}")
4.![\sqrt[n]{ \frac{a}{b}}= \frac{ \sqrt[n]{a}}{ \sqrt[n]{b}}](https://s0.wp.com/latex.php?latex=%5Csqrt%5Bn%5D%7B+%5Cfrac%7Ba%7D%7Bb%7D%7D%3D+%5Cfrac%7B+%5Csqrt%5Bn%5D%7Ba%7D%7D%7B+%5Csqrt%5Bn%5D%7Bb%7D%7D&bg=ffffff&fg=555555&s=1 "\sqrt[n]{ \frac{a}{b}}= \frac{ \sqrt[n]{a}}{ \sqrt[n]{b}}")
, tentu b tidak boleh 0
Pangkat Rasional
Untuk sebarang bilangan real a dan bilangan asli m dan n, dengan n lebih besar atau sama dengan 2, dimana![\sqrt[n]{a}](https://s0.wp.com/latex.php?latex=%5Csqrt%5Bn%5D%7Ba%7D&bg=ffffff&fg=555555&s=0 "\sqrt[n]{a}")
ada, maka
5.![a^{ \frac{1}{n}}= \sqrt[n]{a}](https://s0.wp.com/latex.php?latex=a%5E%7B+%5Cfrac%7B1%7D%7Bn%7D%7D%3D+%5Csqrt%5Bn%5D%7Ba%7D&bg=ffffff&fg=555555&s=1 "a^{ \frac{1}{n}}= \sqrt[n]{a}")
6.![a^{ \frac{m}{n}}= \sqrt[n]{a^m}=( \sqrt[n]{a})^m](https://s0.wp.com/latex.php?latex=a%5E%7B+%5Cfrac%7Bm%7D%7Bn%7D%7D%3D+%5Csqrt%5Bn%5D%7Ba%5Em%7D%3D%28+%5Csqrt%5Bn%5D%7Ba%7D%29%5Em&bg=ffffff&fg=555555&s=1 "a^{ \frac{m}{n}}= \sqrt[n]{a^m}=( \sqrt[n]{a})^m")
7.
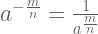
Dari beberapa definisi dan sifat yang diberikan, maka kita bisa menyimpulkan, bahwa menyederhanakan pangkat itu tidak diperbolehkan. Perhatikan sifat
Jika a dan b sebarang bilangan real dan sebarang bilangan asli m dan n (dengan n tidak sama dengan 1), maka
1. Jika n genap, maka
2. jika n ganjil, maka
Bentuk tersebut sama dengan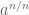
, jika disederhanakan, maka menjadi 
Tentu saja ini tidak bolaeh dilakukan.
Sehingga, jangan menyederhanakan pangkat.
Berapakah
dan berapakah 
Untuk yang pertama,
Kita tahu bahwa
, sehingga bisa dituliskan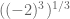 
Dengan menggunakan sifat (perhatikan sifat yang nomor 2) jika n ganjil, maka jawabannya adalah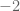
Untuk yang kedua,
Banyak cara yang bisa dilakukan. Misalnya,![(-8)^{2/6}= \sqrt[6]{(-8)^2}= \sqrt[6]{64}=2](https://s0.wp.com/latex.php?latex=%28-8%29%5E%7B2%2F6%7D%3D+%5Csqrt%5B6%5D%7B%28-8%29%5E2%7D%3D+%5Csqrt%5B6%5D%7B64%7D%3D2&bg=ffffff&fg=555555&s=0 "(-8)^{2/6}= \sqrt[6]{(-8)^2}= \sqrt[6]{64}=2")
Cara yang lainnya misalnya,
Cara yang salah. jangan ditiru.
disederhanakan pangkatnya menjadi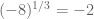 
Ini jelas salah. jangan ditiru.
Latihan :
1.
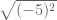
2.![\sqrt[3]{(-5)^3}](https://s0.wp.com/latex.php?latex=%5Csqrt%5B3%5D%7B%28-5%29%5E3%7D&bg=ffffff&fg=555555&s=0 "\sqrt[3]{(-5)^3}")
3.
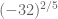
. Dengan mudah kita bisa menjawab, bahwa sesuai definisi yang diberikan, makaKemudian kita ditanya lagi, berapakah nilai dari
. Bagaimana kita menjawabnya?Baca Juga
Sebelum masuk ke pangkat rasional. Tentunya kita harus tahu apa itu pangkat rasional terlebih dahulu. Pangkat rasional adalah bentuk pangkat pecahan. Rasio adalah perbandingan. Jadi,
pangkatnya itu berupa pecahan.
Sebelum kita masuk ke situ, mari kita lihat dulu beberapa sifat penting mengenai bentuk akar.
1. Jika n genap, maka
2. jika n ganjil, maka
3.
4.
, tentu b tidak boleh 0Pangkat Rasional
Untuk sebarang bilangan real a dan bilangan asli m dan n, dengan n lebih besar atau sama dengan 2, dimana
ada, maka5.
6.
7.
Dari beberapa definisi dan sifat yang diberikan, maka kita bisa menyimpulkan, bahwa menyederhanakan pangkat itu tidak diperbolehkan. Perhatikan sifat
Jika a dan b sebarang bilangan real dan sebarang bilangan asli m dan n (dengan n tidak sama dengan 1), maka
1. Jika n genap, maka
2. jika n ganjil, maka
Bentuk tersebut sama dengan
, jika disederhanakan, maka menjadi Tentu saja ini tidak bolaeh dilakukan.
Sehingga, jangan menyederhanakan pangkat.
Berapakah
dan berapakah Untuk yang pertama,
Kita tahu bahwa
, sehingga bisa dituliskan Dengan menggunakan sifat (perhatikan sifat yang nomor 2) jika n ganjil, maka jawabannya adalah
Untuk yang kedua,
Banyak cara yang bisa dilakukan. Misalnya,
Cara yang lainnya misalnya,
Cara yang salah. jangan ditiru.
disederhanakan pangkatnya menjadi Ini jelas salah. jangan ditiru.
Latihan :
1.
2.
3.
0 Response to "Bentuk pangkat rasional"
Posting Komentar
Harap komentar yang bijak!!!