Bilangan kompleks dan sifat-sifatnya
Bilangan kompleks dituliskan sebagai 
Jika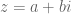 merupakan suatu bilangan kompleks, maka a adalah bagian nyata dan b
adalah bagian imajiner. Ingat a dan b di sini adalah bilangan real.
merupakan suatu bilangan kompleks, maka a adalah bagian nyata dan b
adalah bagian imajiner. Ingat a dan b di sini adalah bilangan real.
Jadi bisa dituliskan
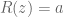 dan
dan 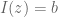
Jika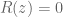 dan
dan 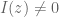 maka disebut bilangan kompleks murni
maka disebut bilangan kompleks murni
Jika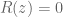 dan
dan 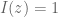 atau dituliskan sebagai
atau dituliskan sebagai 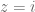 disebut satuan khayal
disebut satuan khayal
Kesamaan bilangan kompleks
Jika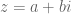 , maka
, maka 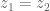 yaitu jika
yaitu jika
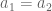 dan
dan 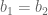
Jumlah pada bilangan kompleks yaitu
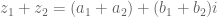
Perkaliannya
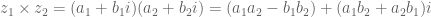
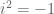
Di dalam bilangan kompleks juga dikenal bilangan nol, yaitu merupakan identitas penjumlahan, yaitu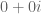
Dan identitas perkaliannya adalah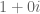
Lawan penjumlahannya,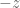
Jika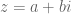 maka
maka 
Kebalikan dari z, yaitu
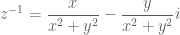
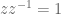
Sekawan (Conjugation)
Jika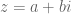 adalah bilangan kompleks, maka sekawannya (conjugation) dari z adalah
adalah bilangan kompleks, maka sekawannya (conjugation) dari z adalah 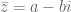
Sifat-sifat bilangan kompleks
Komutatif
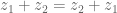

Asosiatif
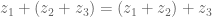
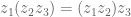
Distributif
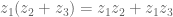
Distributivitas kesekawanan
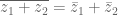
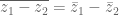
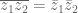
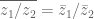
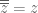
![z \bar z=[R(z)]^2+[I(z)]^2 z \bar z=[R(z)]^2+[I(z)]^2](https://s0.wp.com/latex.php?latex=z+%5Cbar+z%3D%5BR%28z%29%5D%5E2%2B%5BI%28z%29%5D%5E2&bg=ffffff&fg=555555&s=0)
Beberapa soal :
Tuliskan dalam bentuk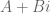 untuk
untuk 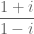
Jawaban :
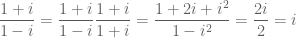
Maka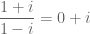
Pangkat bulat tak negatif pada bilangan kompleks didefinisikan seperti pada bilangan nyata, yaitu
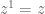
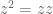
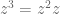

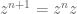
Dan bila , maka
, maka 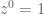
Jika
Jadi bisa dituliskan
Jika
Jika
Kesamaan bilangan kompleks
Jika
Jumlah pada bilangan kompleks yaitu
Perkaliannya
Di dalam bilangan kompleks juga dikenal bilangan nol, yaitu merupakan identitas penjumlahan, yaitu
Dan identitas perkaliannya adalah
Lawan penjumlahannya,
Jika
Kebalikan dari z, yaitu
Sekawan (Conjugation)
Jika
Sifat-sifat bilangan kompleks
Komutatif
Asosiatif
Distributif
Distributivitas kesekawanan
Beberapa soal :
Tuliskan dalam bentuk
Jawaban :
Maka
Pangkat bulat tak negatif pada bilangan kompleks didefinisikan seperti pada bilangan nyata, yaitu
Dan bila
0 Response to "Bilangan kompleks dan sifat-sifatnya"
Posting Komentar
Harap komentar yang bijak!!!