Measure Theory (Teori Ukuran) [Ukuran Luar dan Ukuran Dalam]
Definisi :
Suatu Ukuran Luar dari suatu interval I pada garis bilangan real dengan titik ujung 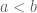 adalah
adalah  dan dinotasikan sebagai
dan dinotasikan sebagai 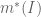
Definisi :
Suatu Ukuran Luar dari suatu himpunan terbuka
dari suatu himpunan terbuka  adalah diberikan oleh
adalah diberikan oleh  dimana
dimana  adalah bentuk dari dekomposisi tunggal dari G kedalam suatu gabungan
dari pasangan-pasangan selang terbuka yang saling bebas baik finite
maupun countably finite
adalah bentuk dari dekomposisi tunggal dari G kedalam suatu gabungan
dari pasangan-pasangan selang terbuka yang saling bebas baik finite
maupun countably finite
Definisi
Ukuran Luar dari sebarang himpunan
dari sebarang himpunan 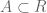 adalah diberikan oleh
adalah diberikan oleh 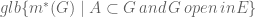
Definisi
Ukuran Dalam dari sebarang himpunan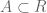 dinotasikan sebagai
dinotasikan sebagai 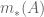 didefinisikan sebagai
didefinisikan sebagai  dimana
dimana  adalah suatu himpunan E tanpa himpunan A.
adalah suatu himpunan E tanpa himpunan A.
Contoh :
Jika ada himpunan berapakah
berapakah 
Jawab :
Tentu saja
Bagaimana dengan![B=(-3, 5] B=(-3, 5]](https://s0.wp.com/latex.php?latex=B%3D%28-3%2C+5%5D&bg=ffffff&fg=555555&s=0) berapakah
berapakah 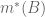
Jawab :
Sama saja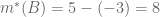
![C=[-3, 5] C=[-3, 5]](https://s0.wp.com/latex.php?latex=C%3D%5B-3%2C+5%5D&bg=ffffff&fg=555555&s=0) berapakah
berapakah 
Jawab :
Maka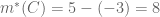
Jika![D=(1, 5) \cup (11, 13] D=(1, 5) \cup (11, 13]](https://s0.wp.com/latex.php?latex=D%3D%281%2C+5%29+%5Ccup+%2811%2C+13%5D&bg=ffffff&fg=555555&s=0) berapakah
berapakah 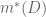
Jawab :
Menggunakan definisi yang kedua :
Maka
Definisi :
Suatu Ukuran Luar
Definisi
Ukuran Luar
Definisi
Ukuran Dalam dari sebarang himpunan
Contoh :
Jika ada himpunan
Jawab :
Tentu saja
Bagaimana dengan
Jawab :
Sama saja
Jawab :
Maka
Jika
Jawab :
Menggunakan definisi yang kedua :
Maka
0 Response to "Measure Theory (Teori Ukuran) [Ukuran Luar dan Ukuran Dalam]"
Posting Komentar
Harap komentar yang bijak!!!