-->
›

Cara cepat mencari hasilnya

By Selasa, 15 September 2015 Add Comment Edit
Berapakah hasil dari (7 \times 8 \times 9 \times 10)+1=?. dengan menghitungnya kita juga bisa mengetahuinya bahwa jumlahnya sama dengan (7 \times 8 \times 9 \times 10)+1=5041=71^2. Tetapi ini cukup membuang waktu kita. Lalu bagaimana cara supaya kita bisa menghitungnya dengan cepat.
Kita tuliskan secara umum. Perkalian empat bilangan asli berurutan ditambah satu. Empat bilangan berurutan bisa dituliskan ke dalam bentuk umumnya yaitu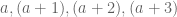 a, (a+1), (a+2), (a+3).
Lalu, kita lakukan proses tersebut :

(a \times (a + 1) \times (a + 2) \times (a + 3)) + 1

Baca Juga

= (a^2 + a)(a^2 + 5a + 6) + 1
= (a^4 + 5a^3 + 6a^2 + a^3 + 5a^2 + 6a) + 1
= a^4 + 6a^3 + 11a^2 + 6a + 1
= a^4 + 2a^2 + 1 + 6a^3 + 9a^2 + 6a
= (a^2 + 1)^2 + 6a(a^2 + 1) + 9a^2
= (a^2 + 1)^2 + 2.(3a)(a^2 + 1) + (3a)^2
= [(a^2 + 1) + 3a]^2

Bentuk terakhir sudah merupakan bentuk kudrat. Jadi, untuk mempercepat kita menghitungnya bisa dilakukan dengan cara mengambil bilangan pertamanya dan memperlakukan seperti itu (bentuk terakhir).



Misalnya
(7 \times 8 \times 9 \times 10)+1?, maka kita bisa menghitungnya dengan bentuk = [(a^2 + 1) + 3a]^2 dengan a sama dengan 7.
Maka didapatkan : = [(7^2 + 1) + 3.7]^2=(50+21)^2=71^2
Selesai.

Tetapi cara menghafalkannya cukup rumit. Kita bisa mengubahnya menjadi seperti berikut ini :
= [(a^2 + 1) + 3a]^2
= [a^2 + 1 + 3a]^2
= [a^2 + 3a + 1]^2
= [a(a+3) + 1]^2

Mungkin cara menghafal yang ini lebih mudah, yaitu angka pertama dikalikan dengan angka terakhirnya.. misalnya,

(a \times (a + 1) \times (a + 2) \times (a + 3)) + 1

(7 \times 8 \times 9 \times 10)+1? didapatkan a=7, \quad (a+3)=10
Dengan cara yang sudah kita dapatkan, maka
= [a(a+3) + 1]^2=(7(10)+1)^2=71^2

Hasilnya sama saja kan..
Semoga bermanfaat.

Related Posts

0 Response to "Cara cepat mencari hasilnya"

Posting Komentar

Harap komentar yang bijak!!!

Langganan: Posting Komentar (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel