Ciri Bilangan habis dibagi 7

  Bila bagian satuannya dikalikan 2, dan menjadi pengurang dari bilangan tersisa. Jika hasilnya habis dibagi 7, maka bilangan itu habis dibagi 7.
Contoh : Apakah 5236 habis dibagi 7?
Kita pisahkan 6 (satuannya), kemudian .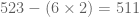

Apakah 511 habis dibagi 7? .
Karena 49 habis dibagi 7, maka 5236 habis dibagi 7.
  
Bukti :
Misalkan bilangan awal adalah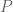
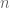  sebanyak digit. Ini adalah bilangan awal.
bedakan dengan yang di atas. Bagian ini berkurang satu digit.
Sehingga diperoleh hubungan antara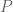 dan 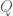, yaitu .

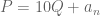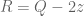  ini adalah syarat bilangan habis dibagi 7.


 
Kita dapat menuliskan syarat bilangan habis dibagi 7 seperti ini : Jika bilangan habis dibagi 7 maka (perhatikan di atas) habis dibagi 7. Jika habis dibagi 7 maka bilangan awal habis dibagi 7.
Dari pernyataan itu bisa dikatakan : “bilangan habis dibagi 7 jika dan hanya jika habis dibagi 7.” Sehingga kita harus membuktikan dua kali. yaitu untuk Jika bilangan habis dibagi 7 maka habis dibagi 7. Dan untuk jika habis dibagi 7 maka bilangan awal habis dibagi 7.
 
#Bukti untuk Jika bilangan habis dibagi 7 maka habis dibagi 7
Bilangan awal yaitu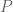 . dan diketahui 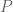habis dibagi 7.
Kita tulis
Contohnya . Artinya habis dibagi . atau adalah faktor dari )


 
Kita punya teorema, jika , maka 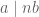dengan 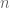bilangan bulat. Sehingga kita boleh menuliskan


 
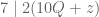
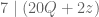
Sekarang perhatikan bahwa 21 habis dibagi 7. Tentunya kelipatan dari 21 juga habis dibagi 7.



 
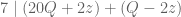
Dalam keterbagian, kita punya teorema jika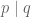 dan maka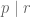
Sehingga diperoleh


 
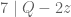
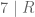
Terbukti
 
 
#Bukti untuk jika habis dibagi 7 maka bilangan awal habis dibagi 7.
 


 
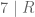
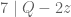
Menurut teorema, jika , maka 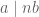dengan 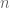bilangan bulat.


 
Seperti halnya bukti yang pertama, 21 habis dibagi 7. Sehingga,




 
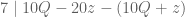
Ada teorema pada keterbagian yang mengatakan, jika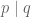 dan maka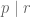

 
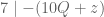
Menurut teorema, ji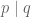ka maka 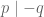. Maka,


 
Terbukti
 
Selanjutnya, Angka 2 ini disebut sebagai Multiplier.
Semoga bermanfaat.

Share this post