Soal dan Solusi #2
Pertanyaan 3
Koto Yunidar
mlm all, bntuin yak,
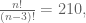 gmana caranya?
gmana caranya?
Jawaban 3
Ali Khan Su’ud
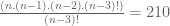
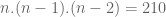
itu bil brurutan.
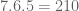

Bagus Kepo Setiadi
 itu kan
itu kan 
 >> berarti berurutan kan
>> berarti berurutan kan
otak atik aja.. alhasil jadi
Pertanyaan 4
Putri Princezna
Tentukan hasil dari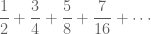
Jawaban 4
Hiyori Hinata
 holds in
holds in  By using termwise differentiation, we get that
By using termwise differentiation, we get that
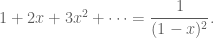
By substituting with
with 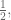 we have
we have

So

Ashfaq Ahmad

Pertanyaan 5
Putri Princezna
Jika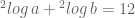 dan
dan  ,
,
maka
Jawaban 5
Purie Astagraha
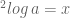
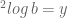





Rusli Gustiono
hmmmm…………
 dan
dan 



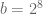
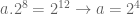


Koto Yunidar
mlm all, bntuin yak,
Jawaban 3
Ali Khan Su’ud
itu bil brurutan.
Bagus Kepo Setiadi
otak atik aja.. alhasil jadi
Pertanyaan 4
Putri Princezna
Tentukan hasil dari
Jawaban 4
Hiyori Hinata
By substituting
So
Ashfaq Ahmad
Pertanyaan 5
Putri Princezna
Jika
maka
Jawaban 5
Purie Astagraha
Rusli Gustiono
hmmmm…………
0 Response to "Soal dan Solusi #2"
Posting Komentar
Harap komentar yang bijak!!!