Menghitung akar tanpa kalkulator (Cara 1)
Sebelumnya ada komentar dari pembaca. Bagaimana cara menghitung akar kuadrat / akar pangkat dua? Kalau mengkuadratkan tinggal dikalikan saja kan. Tetapi kebalikannya? Coba perhatikan bagaimana cara menghitung perkalian, pembagian? Jika pembaca sudah terbiasa dengan menghitung pembagian menggunakan cara “porogapit / paragapit”, (istilah yang saya ketahui sejak SD), mungkin nanti pembaca juga bisa dengan mudah mencari nilai akar kuadrat dengan mudah juga. Oke deh, langsung saja kita bahas, bagaimana cara menemukan nilai akar kuadrat dari suatu bilangan.
Lebih tepatnya, untuk postingan kali ini yaitu menghitung akar pangkat dua tanpa menggunakan kalkulator. Meskipun kalkulator adalah alat canggih yang bisa digunakan untuk melakukan perhitungan matematika dengan cepat, tetapi tidak salah (bahkan dianjurkan) untuk menghitung akar tanpa kalkulator.
Menghitung bentuk akar pangkat dua, atau biasa disebut akar kuadrat untuk beberapa bilangan yang kecil biasanya kita hafal, misalnya akar dari 144. Tentu kita yang sudah biasa akan hafal sendiri diluar kepala. Tetapi bagaimana kalau angka itu cukup besar, ratusan, ribuan, bahkan yang koma-koma (irasional).
Berikut akan sedikit dijelaskan bagaimana cara menghitung akar kuadrat tanpa menggunakan kalkulator atau komputer.
Syaratnya cukup mudah. Pembaca harus hafal nilai kuadrat dari 1 sampai 9. Hehehe.. Cukup mudah kok.
Contoh yang pertama yaitu
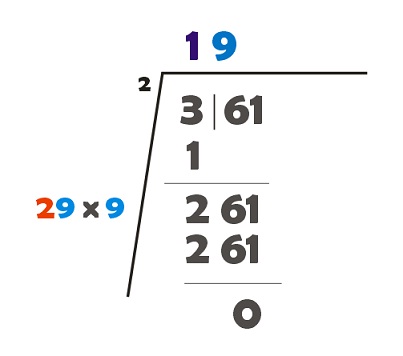
Perhatikan gambar, dan perhatikan juga langkah-langkah berikut ini!
1. Tulis bilangan 361 dengan memisahkannya seperti pada gambar
2. Angka 2 kecil berwarna hitam ini paten (tetap), tidak boleh dirubah.
3. Perhatikan angka 3 pada pemenggalan bilangan 361
4. Bilangan bulat positif berapakah yang jika dikuadratkan maka hasilnya mendekati 3 (tidak boleh melebihi). Tentu bilangan yang dimaksud adalah 1. Tulis di atas, berwarna biru (ini adalah hasil sementara)
5. Seperti biasa (seperti pada pembagian), 3 dikurangi 1 sama dengan 2. Kemudian turunkan 61. Menjadi 261
6. 2 warna merah berasal dari perkalian hasil sementara dengan angka 2 kecil berwarna hitam.
7. “duapuluh berapa dikali berapa” yang hasilnya mendekati 261. (“berapa” di sini haruslah sama. harus yang paling mendekati dengan 261. Tidak boleh melebihi) Ini langkah yang bisa digunakan dengan coba-coba.
8. Tentu akhirnya kita dapatkan angka 9 (berwarna biru muda). Karena
9. Tulis di atas (berwarna biru muda).
10. Karena sudah bersisa 0, maka sudah selesai.
Sehingga hasilnya adalah 19
Mudah bukan!
Pemenggalan bilangan itu harus dua-dua.. dan dipenggal dari belakang..
Misalnya 87645. pemenggalannya yaitu 8|76|45 (Benar)..
Tidak boleh dipenggal menjadi 87|64|5. (Ini salah)
Memenggalnya yaitu sebanyak dua-dua dari belakang. Khusus untuk jumlah digit ganjil yang cukup berbahaya. Karena untuk jumlah digit genap, pemenggalan dari depan dan dari belakang itu sama saja.
Jika ingin memenggal dari depan, hitung dulu jumlah digitnya. Jika jumlah digitnya genap, maka penggal saja dua-dua dari depan.. Jika ternyata jumlah digitnya sebanyak bilangan ganjil. Pemenggalan dari depan boleh dilakukan tetapi harus mengambil satu dulu, baru kemudian dua-dua. (pemenggalan dari depan adalah cara dari Denis Kinta, untuk memudahkan pada soal berikut)
Misalnya kita ingin mencari akar dari 12345678910111213…4950 (Tentu saja tidak mungkin disuruh mencari nilai dari akar ini, karena akan sangat panjang. Biasanya soal seperti ini adalah tentukan 3 angka pertama dari hasil akar tersebut)…
Hitung dulu jumlah digitnya. Karena jumlah digitnya ganjil, maka penggal satu dulu di depan. Sehingga pemenggalannya seperti ini. 1|23|45|67|89|10|11|12|13…
Kita tidak perlu menghitung sampai selesai, sampai ketemu 3 digit pertama sudah selesai…
Contoh lagi yang lebih panjang
Tentukan nilai dari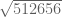
Langkah-langkahnya sebagai berikut :
1. Penggal dulu seperti yang sudah dijelaskan
2. Carilah, berapakah suatu bilangan bulat positif yang jika dikuadratkan hasilnya mendekati 51. Yaitu 7. Karena 7 kuadrat adalah 49. Sedangkan 8 melebihi. Tulis 7 di atas (warna hitam. Ini adalah hasil sementara)
3. Lakukan pengurangan. 51-49=2. Kemudian turunkan 26. Sehingga diperoleh bilanga 226 (warna pink)
4. Selanjutnya tulis 14. Berasal dari hasil sementara dikalikan 2. Hasil sementara kita tadi adalah 7.
5. “Seratus empat puluh berapa dikali berapa” yang hasilnya mendekati 226. (“berapa” di sini haruslah sama. harus yang paling mendekati dengan 226. Tidak boleh melebihi) Ini langkah yang bisa digunakan dengan coba-coba.
6. Diperoleh angka 1. Karena jika kita mengambil 2, maka
dan 284 ini melebihi 226. Sehingga yang memenuhi adalah 1. Tulis angka 1 berwarna hijau di atas. (sehingga hasil sementara yang baru adalah 71)
7. Tuliskan hasil dari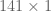
di bawah 226 yang berwarna pink. Kemudian kurangkan sehingga diperoleh 85. Dan turunkan 56 dari atas. Sehingga diperoleh 8556 (berwarna kuning)
8. Sekarang 142 (berwarna biru tua) berasal dari hasil sementara yang baru dikalikan dengan 2. Yaitu
9. “Seribu empat ratus dua puluh berapa dikali berapa” yang hasilnya mendekati 8556. (“berapa” di sini haruslah sama. harus yang paling mendekati dengan 8556. Tidak boleh melebihi) Ini langkah yang bisa digunakan dengan coba-coba.
10. Diperoleh yaitu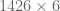
, hasilnya pas yaitu 8556.
11. Tulis angka 6 di atas.
Dan diperoleh hasil akhir yaitu 716.
Dua contoh sudah kita lalui. Apakah ada pertanyaan?
Saya saja tanya sendiri. Hehehe.. Kok dari tadi hasilnya bagus-bagus (merupakan bilangan bulat)? Apakah tidak bisa digunakan untuk bilangan yang hasilnya desimal (ada koma-komanya)?
Jawab : Bisa. (hehehe.. singkat bener ya jawabannya)
Berikut adalah contoh yang hasilnya berupa bilangan desimal. Untuk langkah-langkahnya diserahkan kepada pembaca. Jika kebingungan silahkan lemparkan di komentar
Hitunglah nilai dari
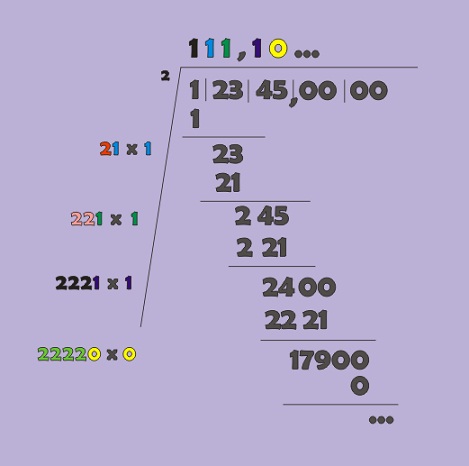
Hasilnya
Ada kelanjutannya, silahkan dicoba ya…
Sebagai latihan, Hitunglah!
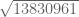dan carilah 3 angka pertama dari 
Selamat mencoba…
Salam Asimtot…
Lebih tepatnya, untuk postingan kali ini yaitu menghitung akar pangkat dua tanpa menggunakan kalkulator. Meskipun kalkulator adalah alat canggih yang bisa digunakan untuk melakukan perhitungan matematika dengan cepat, tetapi tidak salah (bahkan dianjurkan) untuk menghitung akar tanpa kalkulator.
Menghitung bentuk akar pangkat dua, atau biasa disebut akar kuadrat untuk beberapa bilangan yang kecil biasanya kita hafal, misalnya akar dari 144. Tentu kita yang sudah biasa akan hafal sendiri diluar kepala. Tetapi bagaimana kalau angka itu cukup besar, ratusan, ribuan, bahkan yang koma-koma (irasional).
Berikut akan sedikit dijelaskan bagaimana cara menghitung akar kuadrat tanpa menggunakan kalkulator atau komputer.
Syaratnya cukup mudah. Pembaca harus hafal nilai kuadrat dari 1 sampai 9. Hehehe.. Cukup mudah kok.
Contoh yang pertama yaitu
Perhatikan gambar, dan perhatikan juga langkah-langkah berikut ini!
1. Tulis bilangan 361 dengan memisahkannya seperti pada gambar
2. Angka 2 kecil berwarna hitam ini paten (tetap), tidak boleh dirubah.
3. Perhatikan angka 3 pada pemenggalan bilangan 361
4. Bilangan bulat positif berapakah yang jika dikuadratkan maka hasilnya mendekati 3 (tidak boleh melebihi). Tentu bilangan yang dimaksud adalah 1. Tulis di atas, berwarna biru (ini adalah hasil sementara)
5. Seperti biasa (seperti pada pembagian), 3 dikurangi 1 sama dengan 2. Kemudian turunkan 61. Menjadi 261
6. 2 warna merah berasal dari perkalian hasil sementara dengan angka 2 kecil berwarna hitam.
7. “duapuluh berapa dikali berapa” yang hasilnya mendekati 261. (“berapa” di sini haruslah sama. harus yang paling mendekati dengan 261. Tidak boleh melebihi) Ini langkah yang bisa digunakan dengan coba-coba.
8. Tentu akhirnya kita dapatkan angka 9 (berwarna biru muda). Karena
9. Tulis di atas (berwarna biru muda).
10. Karena sudah bersisa 0, maka sudah selesai.
Sehingga hasilnya adalah 19
Mudah bukan!
Pemenggalan bilangan itu harus dua-dua.. dan dipenggal dari belakang..
Misalnya 87645. pemenggalannya yaitu 8|76|45 (Benar)..
Tidak boleh dipenggal menjadi 87|64|5. (Ini salah)
Memenggalnya yaitu sebanyak dua-dua dari belakang. Khusus untuk jumlah digit ganjil yang cukup berbahaya. Karena untuk jumlah digit genap, pemenggalan dari depan dan dari belakang itu sama saja.
Jika ingin memenggal dari depan, hitung dulu jumlah digitnya. Jika jumlah digitnya genap, maka penggal saja dua-dua dari depan.. Jika ternyata jumlah digitnya sebanyak bilangan ganjil. Pemenggalan dari depan boleh dilakukan tetapi harus mengambil satu dulu, baru kemudian dua-dua. (pemenggalan dari depan adalah cara dari Denis Kinta, untuk memudahkan pada soal berikut)
Misalnya kita ingin mencari akar dari 12345678910111213…4950 (Tentu saja tidak mungkin disuruh mencari nilai dari akar ini, karena akan sangat panjang. Biasanya soal seperti ini adalah tentukan 3 angka pertama dari hasil akar tersebut)…
Hitung dulu jumlah digitnya. Karena jumlah digitnya ganjil, maka penggal satu dulu di depan. Sehingga pemenggalannya seperti ini. 1|23|45|67|89|10|11|12|13…
Kita tidak perlu menghitung sampai selesai, sampai ketemu 3 digit pertama sudah selesai…
Contoh lagi yang lebih panjang
Tentukan nilai dari
Langkah-langkahnya sebagai berikut :
1. Penggal dulu seperti yang sudah dijelaskan
2. Carilah, berapakah suatu bilangan bulat positif yang jika dikuadratkan hasilnya mendekati 51. Yaitu 7. Karena 7 kuadrat adalah 49. Sedangkan 8 melebihi. Tulis 7 di atas (warna hitam. Ini adalah hasil sementara)
3. Lakukan pengurangan. 51-49=2. Kemudian turunkan 26. Sehingga diperoleh bilanga 226 (warna pink)
4. Selanjutnya tulis 14. Berasal dari hasil sementara dikalikan 2. Hasil sementara kita tadi adalah 7.
5. “Seratus empat puluh berapa dikali berapa” yang hasilnya mendekati 226. (“berapa” di sini haruslah sama. harus yang paling mendekati dengan 226. Tidak boleh melebihi) Ini langkah yang bisa digunakan dengan coba-coba.
6. Diperoleh angka 1. Karena jika kita mengambil 2, maka
dan 284 ini melebihi 226. Sehingga yang memenuhi adalah 1. Tulis angka 1 berwarna hijau di atas. (sehingga hasil sementara yang baru adalah 71)7. Tuliskan hasil dari
di bawah 226 yang berwarna pink. Kemudian kurangkan sehingga diperoleh 85. Dan turunkan 56 dari atas. Sehingga diperoleh 8556 (berwarna kuning)8. Sekarang 142 (berwarna biru tua) berasal dari hasil sementara yang baru dikalikan dengan 2. Yaitu
9. “Seribu empat ratus dua puluh berapa dikali berapa” yang hasilnya mendekati 8556. (“berapa” di sini haruslah sama. harus yang paling mendekati dengan 8556. Tidak boleh melebihi) Ini langkah yang bisa digunakan dengan coba-coba.
10. Diperoleh yaitu
, hasilnya pas yaitu 8556.11. Tulis angka 6 di atas.
Dan diperoleh hasil akhir yaitu 716.
Dua contoh sudah kita lalui. Apakah ada pertanyaan?
Saya saja tanya sendiri. Hehehe.. Kok dari tadi hasilnya bagus-bagus (merupakan bilangan bulat)? Apakah tidak bisa digunakan untuk bilangan yang hasilnya desimal (ada koma-komanya)?
Jawab : Bisa. (hehehe.. singkat bener ya jawabannya)
Berikut adalah contoh yang hasilnya berupa bilangan desimal. Untuk langkah-langkahnya diserahkan kepada pembaca. Jika kebingungan silahkan lemparkan di komentar
Hitunglah nilai dari
Hasilnya
Ada kelanjutannya, silahkan dicoba ya…
Sebagai latihan, Hitunglah!
dan carilah 3 angka pertama dari Selamat mencoba…
Salam Asimtot…
0 Response to "Menghitung akar tanpa kalkulator (Cara 1)"
Posting Komentar
Harap komentar yang bijak!!!