Bilangan irasional + bilangan irasional

Coba tebak, apa hasil dari penjumlahan dua bilangan irasional? Tebak-tebak saja dulu.
Misalnya






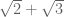
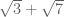
Jika bentuk-bentuk tersebut kita kerjakan, yang kita dapatkan (hasilnya) juga merupakan bilangan irasional. Tentu ini sangatlah mudah dan sangatlah jelas. Bilangan irasional ditambah dengan bilangan irasional hasilnya adalah bilangan irasional.



Bentuk terakhir merupakan bilangan irasional. Apakah semuanya juga begitu? Bilangan irasional
ditambah bilangan irasional sama dengan bilangan irasional? Tentu kita harus membuktikannya jika kita mengatakan demikian. Tetapi coba kita perhatikan hal ini.

Apakah merupakan bilangan irasional?

Kita pasti menjawabnya “iya”. merupakan bilangan irasional, karena tidak dapat dituliskan ke dalam bentuk pecahan. Dan kita juga mengetahuinya bahwa 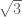juga merupakan bilangan irasional. Lalu, bagaimana dengan hasil penjumlahan dua bilangan irasional berikut?



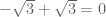
0 adalah bilangan rasional. Karena 0 bisa dituliskan menjadi dengan a dan b bilangan bulat dan b tidak sama dengan nol. Sehingga kita bisa menyimpulkan bahwa, penjumlahan dua bilangan irasional belum tentu menghasilkan bilangan irasional.
Memang, hanya bentuk seperti itu yang menghasilkan bilangan rasional. Hanya bilangan nol yang bisa dihasilkan sebagai bilangan rasional. Bentuk-bentuk dengan bilangan irasional berbeda pasti menghasilkan bilangan irasional juga.

Share this post