Menghitung akar tanpa kalkulator (menggunakan rumus) [pendekatan]
Jika kemarin kita sudah belajar menghitung akar pangkat dua (akar
kuadrat) dengan menggunakan cara yang diajarkan di SD (mungkin cara yang
dari SD ini cukup rumit untuk dilakukan), sekarang kita akan belajar
menghitung nilai dari akar kuadrat dengan menggunakan rumus. Sehingga
akan lebih mudah untuk dilakukan. (tergantung pembaca mau menggunakan
yang lebih mudah yang mana).
Iseng-iseng baca bukunya David Darling yang judulnya The Universal
Book of Mathematics. Di dalamnya ada subjudul yaitu “Bakhshali
manuscript”

Entah itu apa artinya, tetapi ada rumus yang menarik untuk saya pelajari. Akhirnya saya pelajari rumus tersebut dan berikut laporannya :
Hasil dari perhitungan akar kuadrat dengan menggunakan rumus ini sangat mendekati dengan hasil sebenarnya.
Rumusnya adalah sebagai berikut :
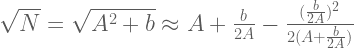
Dengan, N adalah sebarang bilangan asli atau bilangan cacah
A adalah bilangan asli yang jika dikuadratkan nilainya sangat mendekati N
Dan b adalah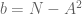
Misalnya untuk menghitung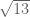 , maka kita pilih
, maka kita pilih 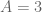 sehingga
sehingga 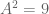 sangat mendekati 13. Sehingga,
sangat mendekati 13. Sehingga, 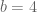 , maka
, maka
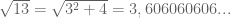
Nilai yang sebenarnya adalah
Berikut ini adalah beberapa nilai untuk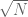 sampai dengan
sampai dengan 
Selisih terbesarnya ada pada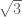 , yaitu mempunyai selisih 0,017949192
, yaitu mempunyai selisih 0,017949192
Selisih terbesar kedua ada pada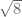 , yaitu mempunyai selisih 0,004906209
, yaitu mempunyai selisih 0,004906209
Jika diperhatikan, dengan menggunakan rumus tersebut. Nilai dari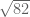 mempunyai tingkat ketelitian yang bagus dibandingkan nilai dari
mempunyai tingkat ketelitian yang bagus dibandingkan nilai dari 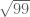 . Begitu juga untuk
. Begitu juga untuk  dengan
dengan 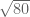 . Begitu juga
. Begitu juga 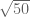 dibandingkan dengan
dibandingkan dengan 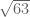 .
.
Jika yang kita hitung adalah yang kurang dari dan mendekati suatu kuadrat sempurna, maka tingkat ketelitiannya kurang bagus. Berbeda dengan jika yang kita hitung adalah yang lebih besar dari dan mendekati suatu kuadrat sempurna. Tingkat ketelitiannya sangatlah bagus.
Untuk menyiasati hal ini, kami mencoba untuk mengambil kasus jika nilai melebihi dari nilai N tetapi masih sangat dekat dengan N, tentu nilai b akan negatif.
melebihi dari nilai N tetapi masih sangat dekat dengan N, tentu nilai b akan negatif.
Beberapa tabelnya untuk N mulai dari 81 sampai 100 adalah sebagai berikut :
Dapat kita lihat bahwa Nilai dari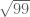 mempunyai tingkat ketelitian yang bagus dibandingkan nilai dari
mempunyai tingkat ketelitian yang bagus dibandingkan nilai dari 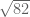
Dan nilai dari suatu kuadrat sempurna itu sendiri jadi tidak sama dengan nilai yang sebenarnya.
Dapat disimpulkan di sini! Untuk mendapatkan nilai dengan ketelitian yang bagus.
Jika kita menghitung suatu bentuk akar yang nilainya sangat mendekati suatu kuadrat sempurna, dan nilainya kurang dari kuadrat sempurna (mendekati dari bawah), maka kita gunakan b dengan nilai negatif. Dan nilai sama dengan bilangan kuadrat sempurna yang didekati.
sama dengan bilangan kuadrat sempurna yang didekati.
Begitu juga sebaliknya.
Intinya! Gunakan nilai A dan b sedemikian sehingga nilai sangat dekat dengan N
sangat dekat dengan N

Baca Juga
Entah itu apa artinya, tetapi ada rumus yang menarik untuk saya pelajari. Akhirnya saya pelajari rumus tersebut dan berikut laporannya :
Hasil dari perhitungan akar kuadrat dengan menggunakan rumus ini sangat mendekati dengan hasil sebenarnya.
Rumusnya adalah sebagai berikut :
Dengan, N adalah sebarang bilangan asli atau bilangan cacah
A adalah bilangan asli yang jika dikuadratkan nilainya sangat mendekati N
Dan b adalah
Misalnya untuk menghitung
Nilai yang sebenarnya adalah
Berikut ini adalah beberapa nilai untuk
| Menggunakan Rumus | ||
| 1 | 1 | 1 |
| 2 | 1,414213562 | 1,416666667 |
| 3 | 1,732050808 | 1,75 |
| 4 | 2 | 2 |
| 5 | 2,236067977 | 2,236111111 |
| 6 | 2,449489743 | 2,45 |
| 7 | 2,645751311 | 2,647727273 |
| 8 | 2,828427125 | 2,833333333 |
| 9 | 3 | 3 |
| 10 | 3,16227766 | 3,162280702 |
| 11 | 3,31662479 | 3,316666667 |
| 12 | 3,464101615 | 3,464285714 |
| 13 | 3,605551275 | 3,606060606 |
| 14 | 3,741657387 | 3,742753623 |
| 15 | 3,872983346 | 3,875 |
| 16 | 4 | 4 |
| 17 | 4,123105626 | 4,123106061 |
| 18 | 4,242640687 | 4,242647059 |
| 19 | 4,358898944 | 4,358928571 |
| 20 | 4,472135955 | 4,472222222 |
| 21 | 4,582575695 | 4,58277027 |
| 22 | 4,69041576 | 4,690789474 |
| 23 | 4,795831523 | 4,796474359 |
| 24 | 4,898979486 | 4,9 |
| 25 | 5 | 5 |
| 26 | 5,099019514 | 5,099019608 |
| 27 | 5,196152423 | 5,196153846 |
| 28 | 5,291502622 | 5,291509434 |
| 29 | 5,385164807 | 5,385185185 |
| 30 | 5,477225575 | 5,477272727 |
| 31 | 5,567764363 | 5,567857143 |
| 32 | 5,656854249 | 5,657017544 |
| 33 | 5,744562647 | 5,744827586 |
| 34 | 5,830951895 | 5,831355932 |
| 35 | 5,916079783 | 5,916666667 |
| 36 | 6 | 6 |
| 37 | 6,08276253 | 6,082762557 |
| 38 | 6,164414003 | 6,164414414 |
| 39 | 6,244997998 | 6,245 |
| 40 | 6,32455532 | 6,324561404 |
| 41 | 6,403124237 | 6,403138528 |
| 42 | 6,480740698 | 6,480769231 |
| 43 | 6,557438524 | 6,557489451 |
| 44 | 6,633249581 | 6,633333333 |
| 45 | 6,708203932 | 6,708333333 |
| 46 | 6,782329983 | 6,782520325 |
| 47 | 6,8556546 | 6,855923695 |
| 48 | 6,92820323 | 6,928571429 |
| 49 | 7 | 7 |
| 50 | 7,071067812 | 7,071067821 |
| 51 | 7,141428429 | 7,141428571 |
| 52 | 7,211102551 | 7,211103253 |
| 53 | 7,280109889 | 7,280112045 |
| 54 | 7,348469228 | 7,348474341 |
| 55 | 7,416198487 | 7,416208791 |
| 56 | 7,483314774 | 7,483333333 |
| 57 | 7,549834435 | 7,549865229 |
| 58 | 7,615773106 | 7,615821095 |
| 59 | 7,681145748 | 7,681216931 |
| 60 | 7,745966692 | 7,746068152 |
| 61 | 7,810249676 | 7,81038961 |
| 62 | 7,874007874 | 7,874195624 |
| 63 | 7,937253933 | 7,9375 |
| 64 | 8 | 8 |
| 65 | 8,062257748 | 8,062257752 |
| 66 | 8,124038405 | 8,124038462 |
| 67 | 8,185352772 | 8,185353053 |
| 68 | 8,246211251 | 8,246212121 |
| 69 | 8,306623863 | 8,30662594 |
| 70 | 8,366600265 | 8,366604478 |
| 71 | 8,426149773 | 8,426157407 |
| 72 | 8,485281374 | 8,485294118 |
| 73 | 8,544003745 | 8,544023723 |
| 74 | 8,602325267 | 8,602355072 |
| 75 | 8,660254038 | 8,660296763 |
| 76 | 8,717797887 | 8,717857143 |
| 77 | 8,774964387 | 8,775044326 |
| 78 | 8,831760866 | 8,831866197 |
| 79 | 8,888194417 | 8,88833042 |
| 80 | 8,94427191 | 8,944444444 |
| 81 | 9 | 9 |
| 82 | 9,055385138 | 9,05538514 |
| 83 | 9,110433579 | 9,110433604 |
| 84 | 9,16515139 | 9,165151515 |
| 85 | 9,219544457 | 9,219544846 |
| 86 | 9,273618495 | 9,273619428 |
| 87 | 9,327379053 | 9,327380952 |
| 88 | 9,38083152 | 9,380834977 |
| 89 | 9,433981132 | 9,433986928 |
| 90 | 9,486832981 | 9,486842105 |
| 91 | 9,539392014 | 9,539405685 |
| 92 | 9,591663047 | 9,591682723 |
| 93 | 9,643650761 | 9,643678161 |
| 94 | 9,695359715 | 9,695396825 |
| 95 | 9,746794345 | 9,746843434 |
| 96 | 9,797958971 | 9,798022599 |
| 97 | 9,848857802 | 9,848938826 |
| 98 | 9,899494937 | 9,899596524 |
| 99 | 9,949874371 | 9,95 |
Selisih terbesarnya ada pada
Selisih terbesar kedua ada pada
Jika diperhatikan, dengan menggunakan rumus tersebut. Nilai dari
Jika yang kita hitung adalah yang kurang dari dan mendekati suatu kuadrat sempurna, maka tingkat ketelitiannya kurang bagus. Berbeda dengan jika yang kita hitung adalah yang lebih besar dari dan mendekati suatu kuadrat sempurna. Tingkat ketelitiannya sangatlah bagus.
Untuk menyiasati hal ini, kami mencoba untuk mengambil kasus jika nilai
Beberapa tabelnya untuk N mulai dari 81 sampai 100 adalah sebagai berikut :
| Rumus untuk b negatif | ||
| 81 | 9 | 9,000138122 |
| 82 | 9,055385138 | 9,055494505 |
| 83 | 9,110433579 | 9,110519126 |
| 84 | 9,16515139 | 9,165217391 |
| 85 | 9,219544457 | 9,219594595 |
| 86 | 9,273618495 | 9,273655914 |
| 87 | 9,327379053 | 9,327406417 |
| 88 | 9,38083152 | 9,380851064 |
| 89 | 9,433981132 | 9,433994709 |
| 90 | 9,486832981 | 9,486842105 |
| 91 | 9,539392014 | 9,539397906 |
| 92 | 9,591663047 | 9,591666667 |
| 93 | 9,643650761 | 9,64365285 |
| 94 | 9,695359715 | 9,695360825 |
| 95 | 9,746794345 | 9,746794872 |
| 96 | 9,797958971 | 9,797959184 |
| 97 | 9,848857802 | 9,848857868 |
| 98 | 9,899494937 | 9,899494949 |
| 99 | 9,949874371 | 9,949874372 |
| 100 | 10 | 10,00010284 |
Dapat kita lihat bahwa Nilai dari
Dan nilai dari suatu kuadrat sempurna itu sendiri jadi tidak sama dengan nilai yang sebenarnya.
Dapat disimpulkan di sini! Untuk mendapatkan nilai dengan ketelitian yang bagus.
Jika kita menghitung suatu bentuk akar yang nilainya sangat mendekati suatu kuadrat sempurna, dan nilainya kurang dari kuadrat sempurna (mendekati dari bawah), maka kita gunakan b dengan nilai negatif. Dan nilai
Begitu juga sebaliknya.
Intinya! Gunakan nilai A dan b sedemikian sehingga nilai

0 Response to "Menghitung akar tanpa kalkulator (menggunakan rumus) [pendekatan]"
Posting Komentar
Harap komentar yang bijak!!!